CF1228F.One Node is Gone
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You have an integer n . Let's define following tree generation as McDic's generation:
- Make a complete and full binary tree of 2n−1 vertices. Complete and full binary tree means a tree that exactly one vertex is a root, all leaves have the same depth (distance from the root), and all non-leaf nodes have exactly two child nodes.
- Select a non-root vertex v from that binary tree.
- Remove v from tree and make new edges between v 's parent and v 's direct children. If v has no children, then no new edges will be made.
You have a tree. Determine if this tree can be made by McDic's generation. If yes, then find the parent vertex of removed vertex in tree.
输入格式
The first line contains integer n ( 2≤n≤17 ).
The i -th of the next 2n−3 lines contains two integers ai and bi ( 1≤ai<bi≤2n−2 ) — meaning there is an edge between ai and bi . It is guaranteed that the given edges form a tree.
输出格式
Print two lines.
In the first line, print a single integer — the number of answers. If given tree cannot be made by McDic's generation, then print 0 .
In the second line, print all possible answers in ascending order, separated by spaces. If the given tree cannot be made by McDic's generation, then don't print anything.
输入输出样例
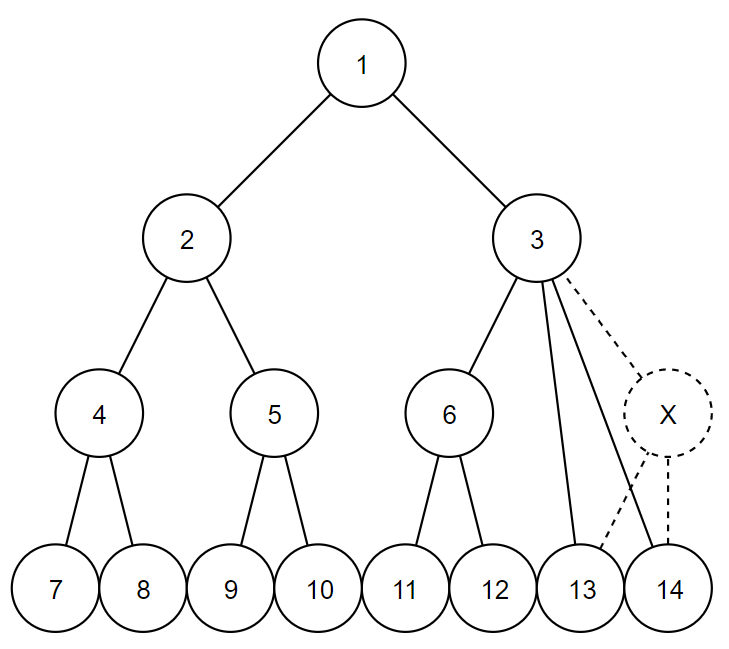
输入#1
4 1 2 1 3 2 4 2 5 3 6 3 13 3 14 4 7 4 8 5 9 5 10 6 11 6 12
输出#1
1 3
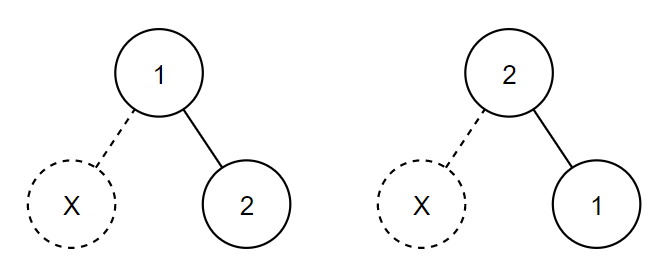
输入#2
2 1 2
输出#2
2 1 2
输入#3
3 1 2 2 3 3 4 4 5 5 6
输出#3
0
说明/提示
In the first example, 3 is the only possible answer.
 In the second example, there are 2 possible answers.
In the second example, there are 2 possible answers.
 In the third example, the tree can't be generated by McDic's generation.
In the third example, the tree can't be generated by McDic's generation.