CF1242E.Planar Perimeter

Ujan has finally cleaned up his house and now wants to decorate the interior. He decided to place a beautiful carpet that would really tie the guest room together.

He is interested in carpets that are made up of polygonal patches such that each side of a patch is either a side of another (different) patch, or is an exterior side of the whole carpet. In other words, the carpet can be represented as a planar graph, where each patch corresponds to a face of the graph, each face is a simple polygon. The perimeter of the carpet is the number of the exterior sides.

Ujan considers a carpet beautiful if it consists of $f$ patches, where the $i$ -th patch has exactly $a_i$ sides, and the perimeter is the smallest possible. Find an example of such a carpet, so that Ujan can order it!

The first line of input contains a single integer $f$ ( $1 \leq f \leq 10^5$ ), the number of patches in the carpet.

The next line contains $f$ integers $a_1, \ldots, a_f$ ( $3 \leq a_i \leq 3\cdot 10^5$ ), the number of sides of the patches. The total number of the sides of the patches $a_1 + \ldots + a_f$ does not exceed $3\cdot10^5$ .

Output the description of the carpet as a graph.

First, output a single integer $n$ ( $3 \leq n \leq 3 \cdot 10^5$ ), the total number of vertices in your graph (the vertices must be numbered from $1$ to $n$ ).

Then output $f$ lines containing the description of the faces. The $i$ -th line should describe the $i$ -th face and contain $a_i$ distinct integers $v_{i,1}, \ldots, v_{i,a_i}$ ( $1 \leq v_{i,j} \leq n$ ), which means that the vertices $v_{i,j}$ and $v_{i,(j \bmod{a_i})+1}$ are connected by an edge for any $1 \leq j \leq a_i$ .

The graph should be planar and satisfy the restrictions described in the problem statement. Its perimeter should be the smallest possible. There should be no double edges or self-loops in the graph. The graph should be connected. Note that a solution always exists; if there are multiple solutions, output any of them.

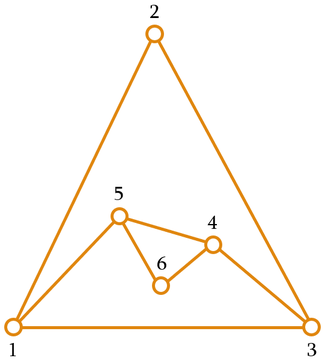
In the first sample, the two triangular faces are connected by a single edge, which results in the minimum perimeter $4$ .

The figure shows one possible configuration for the second sample. The minimum perimeter in this case is $3$ .