CF1200F.Graph Traveler

Gildong is experimenting with an interesting machine Graph Traveler. In Graph Traveler, there is a directed graph consisting of $n$ vertices numbered from $1$ to $n$ . The $i$ -th vertex has $m_i$ outgoing edges that are labeled as $e_i[0]$ , $e_i[1]$ , $\ldots$ , $e_i[m_i-1]$ , each representing the destination vertex of the edge. The graph can have multiple edges and self-loops. The $i$ -th vertex also has an integer $k_i$ written on itself.

A travel on this graph works as follows.

1. Gildong chooses a vertex to start from, and an integer to start with. Set the variable $c$ to this integer.
2. After arriving at the vertex $i$ , or when Gildong begins the travel at some vertex $i$ , add $k_i$ to $c$ .
3. The next vertex is $e_i[x]$ where $x$ is an integer $0 \le x \le m_i-1$ satisfying $x \equiv c \pmod {m_i}$ . Go to the next vertex and go back to step 2.

It's obvious that a travel never ends, since the 2nd and the 3rd step will be repeated endlessly.

For example, assume that Gildong starts at vertex $1$ with $c = 5$ , and $m_1 = 2$ , $e_1[0] = 1$ , $e_1[1] = 2$ , $k_1 = -3$ . Right after he starts at vertex $1$ , $c$ becomes $2$ . Since the only integer $x$ ( $0 \le x \le 1$ ) where $x \equiv c \pmod {m_i}$ is $0$ , Gildong goes to vertex $e_1[0] = 1$ . After arriving at vertex $1$ again, $c$ becomes $-1$ . The only integer $x$ satisfying the conditions is $1$ , so he goes to vertex $e_1[1] = 2$ , and so on.

Since Gildong is quite inquisitive, he's going to ask you $q$ queries. He wants to know how many distinct vertices will be visited infinitely many times, if he starts the travel from a certain vertex with a certain value of $c$ . Note that you should not count the vertices that will be visited only finite times.

The first line of the input contains an integer $n$ ( $1 \le n \le 1000$ ), the number of vertices in the graph.

The second line contains $n$ integers. The $i$ -th integer is $k_i$ ( $-10^9 \le k_i \le 10^9$ ), the integer written on the $i$ -th vertex.

Next $2 \cdot n$ lines describe the edges of each vertex. The $(2 \cdot i + 1)$ -st line contains an integer $m_i$ ( $1 \le m_i \le 10$ ), the number of outgoing edges of the $i$ -th vertex. The $(2 \cdot i + 2)$ -nd line contains $m_i$ integers $e_i[0]$ , $e_i[1]$ , $\ldots$ , $e_i[m_i-1]$ , each having an integer value between $1$ and $n$ , inclusive.

Next line contains an integer $q$ ( $1 \le q \le 10^5$ ), the number of queries Gildong wants to ask.

Next $q$ lines contains two integers $x$ and $y$ ( $1 \le x \le n$ , $-10^9 \le y \le 10^9$ ) each, which mean that the start vertex is $x$ and the starting value of $c$ is $y$ .

For each query, print the number of distinct vertices that will be visited infinitely many times, if Gildong starts at vertex $x$ with starting integer $y$ .

The first example can be shown like the following image:

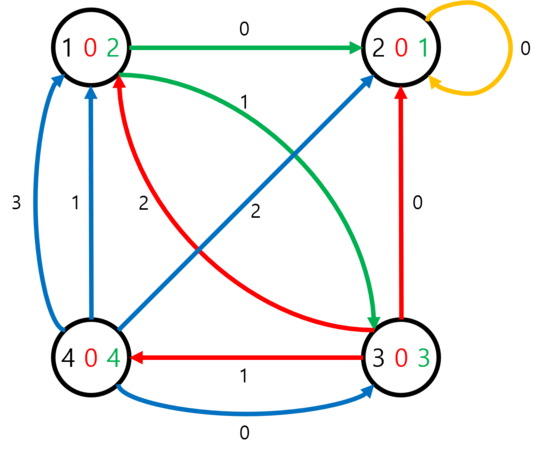Three integers are marked on $i$ -th vertex: $i$ , $k_i$ , and $m_i$ respectively. The outgoing edges are labeled with an integer representing the edge number of $i$ -th vertex.

The travel for each query works as follows. It is described as a sequence of phrases, each in the format "vertex ( $c$ after $k_i$ added)".

• $1(0) \to 2(0) \to 2(0) \to \ldots$
• $2(0) \to 2(0) \to \ldots$
• $3(-1) \to 1(-1) \to 3(-1) \to \ldots$
• $4(-2) \to 2(-2) \to 2(-2) \to \ldots$
• $1(1) \to 3(1) \to 4(1) \to 1(1) \to \ldots$
• $1(5) \to 3(5) \to 1(5) \to \ldots$

The second example is same as the first example, except that the vertices have non-zero values. Therefore the answers to the queries also differ from the first example.

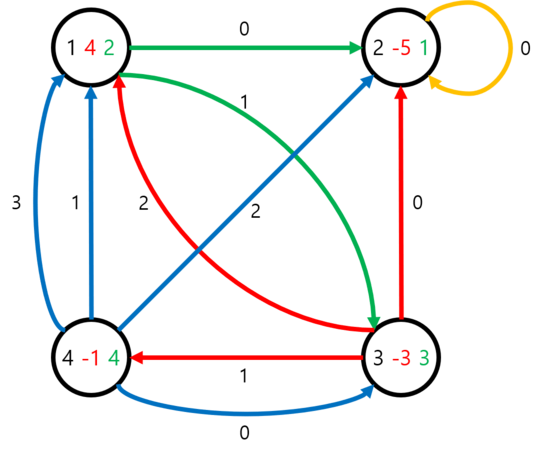The queries for the second example works as follows:

• $1(4) \to 2(-1) \to 2(-6) \to \ldots$
• $2(-5) \to 2(-10) \to \ldots$
• $3(-4) \to 1(0) \to 2(-5) \to 2(-10) \to \ldots$
• $4(-3) \to 1(1) \to 3(-2) \to 4(-3) \to \ldots$
• $1(5) \to 3(2) \to 1(6) \to 2(1) \to 2(-4) \to \ldots$
• $1(9) \to 3(6) \to 2(1) \to 2(-4) \to \ldots$