CF1188A2.Add on a Tree: Revolution

Note that this is the second problem of the two similar problems. You can hack this problem if you solve it. But you can hack the previous problem only if you solve both problems.

You are given a tree with $n$ nodes. In the beginning, $0$ is written on all edges. In one operation, you can choose any $2$ distinct leaves $u$ , $v$ and any integer number $x$ and add $x$ to values written on all edges on the simple path between $u$ and $v$ . Note that in previous subtask $x$ was allowed to be any real, here it has to be integer.

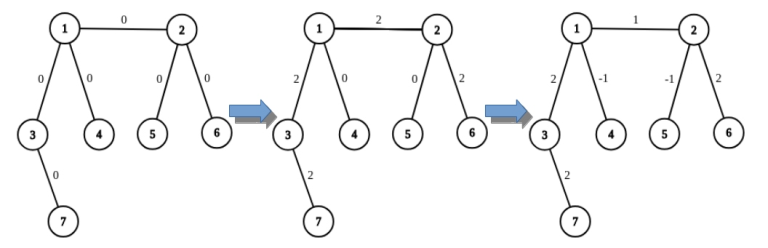
For example, on the picture below you can see the result of applying two operations to the graph: adding $2$ on the path from $7$ to $6$ , and then adding $-1$ on the path from $4$ to $5$ .

You are given some configuration of nonnegative integer pairwise different even numbers, written on the edges. For a given configuration determine if it is possible to achieve it with these operations, and, if it is possible, output the sequence of operations that leads to the given configuration. Constraints on the operations are listed in the output format section.

Leave is a node of a tree of degree $1$ . Simple path is a path that doesn't contain any node twice.

The first line contains a single integer $n$ ( $2 \le n \le 1000$ ) — the number of nodes in a tree.

Each of the next $n-1$ lines contains three integers $u$ , $v$ , $val$ ( $1 \le u, v \le n$ , $u \neq v$ , $0 \le val \le 10\,000$ ), meaning that there is an edge between nodes $u$ and $v$ with $val$ written on it. It is guaranteed that these edges form a tree. It is guaranteed that all $val$ numbers are pairwise different and even.

If there aren't any sequences of operations which lead to the given configuration, output "NO".

If it exists, output "YES" in the first line. In the second line output $m$ — number of operations you are going to apply ( $0 \le m \le 10^5$ ). Note that you don't have to minimize the number of the operations!

In the next $m$ lines output the operations in the following format:

$u, v, x$ ( $1 \le u, v \le n$ , $u \not = v$ , $x$ — integer, $-10^9 \le x \le 10^9$ ), where $u, v$ — leaves, $x$ — number we are adding.

It is guaranteed that if there exists a sequence of operations producing given configuration, then there exists a sequence of operations producing given configuration, satisfying all the conditions above.

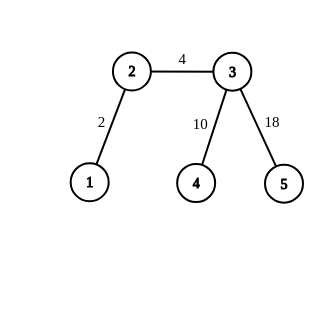
The configuration from the first sample is drawn below, and it is impossible to achieve.

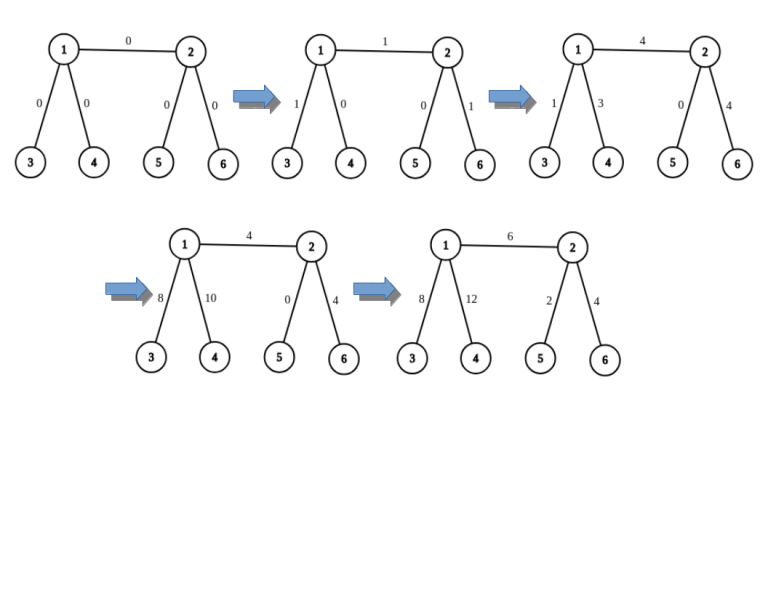
The sequence of operations from the second sample is illustrated below.