CF1190D.Tokitsukaze and Strange Rectangle

There are $n$ points on the plane, the $i$ -th of which is at $(x_i, y_i)$ . Tokitsukaze wants to draw a strange rectangular area and pick all the points in the area.

The strange area is enclosed by three lines, $x = l$ , $y = a$ and $x = r$ , as its left side, its bottom side and its right side respectively, where $l$ , $r$ and $a$ can be any real numbers satisfying that $l < r$ . The upper side of the area is boundless, which you can regard as a line parallel to the $x$ -axis at infinity. The following figure shows a strange rectangular area.

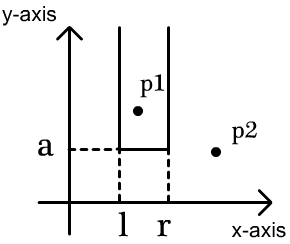A point $(x_i, y_i)$ is in the strange rectangular area if and only if $l < x_i < r$ and $y_i > a$ . For example, in the above figure, $p_1$ is in the area while $p_2$ is not.

Tokitsukaze wants to know how many different non-empty sets she can obtain by picking all the points in a strange rectangular area, where we think two sets are different if there exists at least one point in one set of them but not in the other.

The first line contains a single integer $n$ ( $1 \leq n \leq 2 \times 10^5$ ) — the number of points on the plane.

The $i$ -th of the next $n$ lines contains two integers $x_i$ , $y_i$ ( $1 \leq x_i, y_i \leq 10^9$ ) — the coordinates of the $i$ -th point.

All points are distinct.

Print a single integer — the number of different non-empty sets of points she can obtain.

For the first example, there is exactly one set having $k$ points for $k = 1, 2, 3$ , so the total number is $3$ .

For the second example, the numbers of sets having $k$ points for $k = 1, 2, 3$ are $3$ , $2$ , $1$ respectively, and their sum is $6$ .

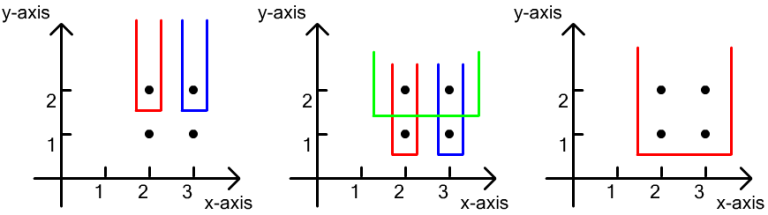
For the third example, as the following figure shows, there are

• $2$ sets having one point;
• $3$ sets having two points;
• $1$ set having four points.

Therefore, the number of different non-empty sets in this example is $2 + 3 + 0 + 1 = 6$ .