CF1192B.Dynamic Diameter

You are given a weighted undirected tree on $n$ vertices and a list of $q$ updates. Each update changes the weight of one edge. The task is to output the diameter of the tree after each update.

(The distance between two vertices is the sum of the weights on the unique simple path that connects them. The diameter is the largest of all those distances.)

The first line contains three space-separated integers $n$ , $q$ and $w$ ( $2 \leq n \leq 100,000, 1 \leq q \leq 100,000$ , $1 \leq w \leq 20,000,000,000,000$ ) – the number of vertices in the tree, the number of updates and the limit on the weights of edges. The vertices are numbered $1$ through $n$ .

Next, $n-1$ lines describing the initial tree follow. The $i$ -th of these lines contains three space-separated integers $a_i$ , $b_i$ , $c_i$ ( $1 \leq a_i, b_i \leq n$ , $0 \leq c_i < w$ ) meaning that initially, there is an edge between vertices $a_i$ and $b_i$ with weight $c_i$ . It is guaranteed that these $n-1$ lines describe a tree.

Finally, $q$ lines describing queries follow. The $j$ -th of these lines contains two space-separated integers $d_j$ , $e_j$ ( $0 \leq d_j < n - 1, 0 \leq e_j < w$ ). These two integers are then transformed according to the following scheme:

• $d'_j = (d_j + last) \bmod (n - 1)$
• $e'_j = (e_j + last) \bmod w$

where $last$ is the result of the last query (initially $last=0$ ). Tuple $(d'_j, e'_j)$ represents a query which takes the $d'_j+1$ -th edge from the input and sets its weight to $e'_j$ .

Output $q$ lines. For each $i$ , line $i$ should contain the diameter of the tree after the $i$ -th update.

Scoring

Subtask 1 (11 points): $n,q \leq 100$ and $w \leq 10,000$

Subtask 2 (13 points): $n,q \leq 5,000$ and $w \leq 10,000$

Subtask 3 (7 points): $w \leq 10,000$ and the edges of the tree are exactly all valid edges of the form $\{1, i\}$ (Hence, the tree is a star centered at vertex 1.)

Subtask 4 (18 points): $w \leq 10,000$ , and the edges of the tree are exactly all valid edges of the forms $\{i, 2i\}$ and $\{i, 2i+1\}$ (Hence, if we were to root the tree at vertex 1, it would be a balanced binary tree.)

Subtask 5 (24 points): it is guaranteed that after each update a longest simple path goes through vertex $1$

Subtask 6 (27 points): no additional constraints

The first sample is depicted in the figure below. The left-most picture shows the initial state of the graph. Each following picture depicts the situation after an update. The weight of the updated edge is painted green, and the diameter is red.

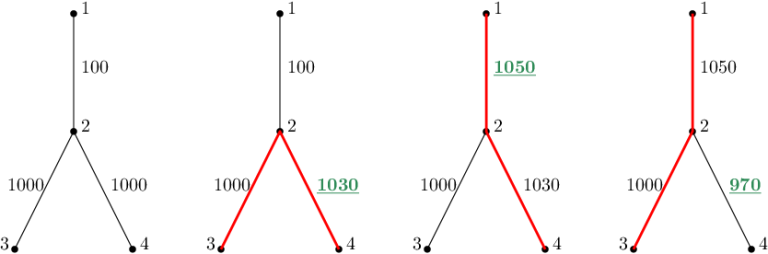
The first query changes the weight of the $3$ rd edge, i.e. $\{2, 4\}$ , to $1030$ . The largest distance between any pair of vertices is $2030$ – the distance between $3$ and $4$ .

As the answer is $2030$ , the second query is

$$d'_2 = (1 + 2030) \bmod 3 = 0$$

$$e'_2 = (1020 + 2030) \bmod 2000 = 1050$$

Hence the weight of the edge $\{1, 2\}$ is changed to $1050$ . This causes the pair $\{1, 4\}$ to be the pair with the greatest distance, namely $2080$ .

The third query is decoded as

$$d'_3 = (1 + 2080) \bmod 3 = 2$$

$$e'_3 = (890 + 2080) \bmod 2000 = 970$$

As the weight of the edge $\{2, 4\}$ decreases to $970$ , the most distant pair is suddenly $\{1, 3\}$ with $2050$
.