CF1193C.Scissors and Tape

The first line contains the source shape $S$ .

The second line contains the target shape $T$ .

Each shape has between 3 and 10 points, inclusive. Both shapes are given in the format specified above.

All coordinates in the input are integers between $-10^6$ and $10^6$ , inclusive.

In each shape, no three points form an angle smaller than 3 degrees. (This includes non-consecutive points and implies that no three points are collinear.)

The polygons $P(S)$ and $P(T)$ have the same area.

Whenever you use the scissors operation, output a block of lines of the form:

<pre class="verbatim"><br></br>scissors<br></br>id(A) k<br></br>B_1<br></br>B_2<br></br>...<br></br>B_k<br></br>

where $id(A)$ is the ID of the shape you want to destroy, $k$ is the number of new shapes you want to produce, and $B_1,\dots,B_k$ are those shapes.

Whenever you use the tape operation, output a block of lines of the form:

<pre class="verbatim"><br></br>tape<br></br>k id(A_1) ... id(A_k)<br></br>C_1<br></br>C_2<br></br>...<br></br>C_k<br></br>B<br></br>

where $k$ is the number of shapes you want to tape together, $id(A_1),\dots,id(A_k)$ are their IDs, $C_1,\dots,C_k$ are equivalent shapes showing their position within $B$ , and $B$ is the final shape obtained by taping them together.

It is recommended to output coordinates of points to at least 10 decimal places.

The output must satisfy the following:

• All coordinates of points in the output must be between $-10^7$ and $10^7$ , inclusive.
• Each shape in the output must have at most $100$ points.
• In each operation the number $k$ of shapes must be between $1$ and $100$ , inclusive.
• The number of operations must not exceed $2000$ .
• The total number of points in all shapes in the output must not exceed $20000$ .
• In the end, there must be exactly one shape (that hasn't been destroyed), and that shape must be equivalent to $T$ .
• All operations must be valid according to the checker. Solutions with small rounding errors will be accepted. (Internally, all comparisons check for absolute or relative error up to $10^{-3}$ when verifying each condition.)

Scoring

A shape is called a nice rectangle if it has the form $((0,0),~ (x,0),~ (x,y),~ (0,y))$ for some positive integers $x$ and $y$ .

A shape is called a nice square if additionally $x=y$ .

A shape $A$ is called strictly convex if all inner angles of the polygon $P(A)$ are smaller than 180 degrees.

Subtask 1 (5 points): $S$ and $T$ are nice rectangles. All coordinates of all points are integers between 0 and 10, inclusive

Subtask 2 (13 points): $S$ is a nice rectangle with $x>y$ , and $T$ is a nice square

Subtask 3 (12 points): $S$ and $T$ are nice rectangles

Subtask 4 (14 points): $S$ is a triangle and $T$ is a nice square

Subtask 5 (10 points): $S$ and $T$ are triangles

Subtask 6 (16 points): $S$ is a strictly convex polygon and $T$ is a nice rectangle

Subtask 7 (11 points): $T$ is a nice rectangle

Subtask 8 (19 points): no additional constraints

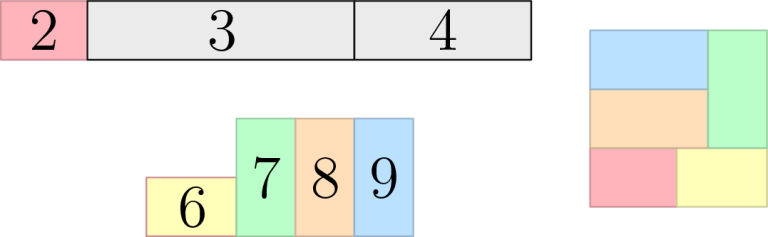
The figure below shows the first example output. On the left is the original figure after using the scissors, on the right are the corresponding $C_i$ when we tape those pieces back together.

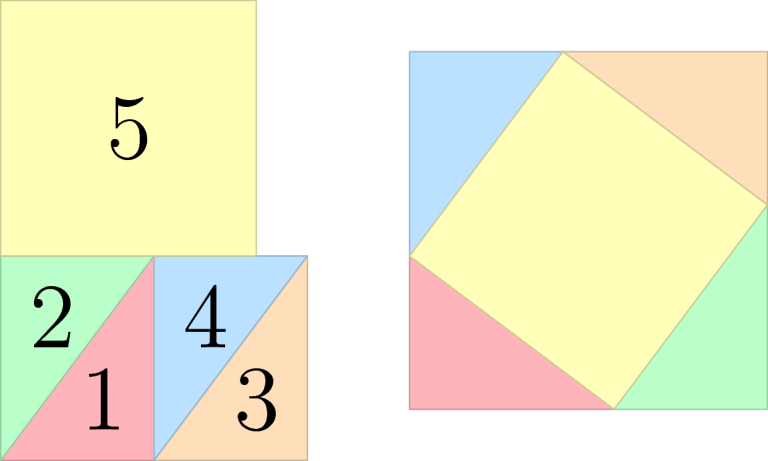
In the second example output, note that it is sufficient if the final shape is equivalent to the target one, they do not have to be identical.

The figure below shows three stages of the third example output. First, we cut the input rectangle into two smaller rectangles, then we cut the bigger of those two rectangles into two more. State after these cuts is shown in the top left part of the figure.

Continuing, we tape the two new rectangles together to form a six-sided polygon, and then we cut that polygon into three 2-by-1 rectangles and one smaller rectangle. This is shown in the bottom left part of the figure.

Finally, we take the rectangle we still have from the first step and the four new rectangles and we assemble them into the desired 3-by-3 square.

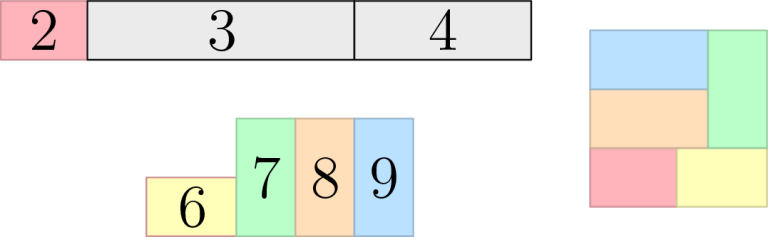
The figure below shows the first example output. On the left is the original figure after using the scissors, on the right are the corresponding $C_i$ when we tape those pieces back together.

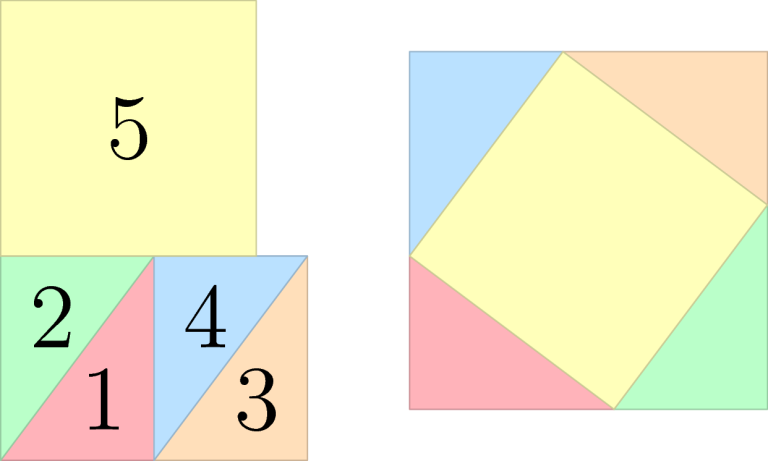
In the second example output, note that it is sufficient if the final shape is equivalent to the target one, they do not have to be identical.

The figure below shows three stages of the third example output. First, we cut the input rectangle into two smaller rectangles, then we cut the bigger of those two rectangles into two more. State after these cuts is shown in the top left part of the figure.

Continuing, we tape the two new rectangles together to form a six-sided polygon, and then we cut that polygon into three 2-by-1 rectangles and one smaller rectangle. This is shown in the bottom left part of the figure.

Finally, we take the rectangle we still have from the first step and the four new rectangles and we assemble them into the desired 3-by-3 square.