CF1173B.Nauuo and Chess

Nauuo is a girl who loves playing chess.

One day she invented a game by herself which needs $n$ chess pieces to play on a $m\times m$ chessboard. The rows and columns are numbered from $1$ to $m$ . We denote a cell on the intersection of the $r$ -th row and $c$ -th column as $(r,c)$ .

The game's goal is to place $n$ chess pieces numbered from $1$ to $n$ on the chessboard, the $i$ -th piece lies on $(r_i,\,c_i)$ , while the following rule is satisfied: for all pairs of pieces $i$ and $j$ , $|r_i-r_j|+|c_i-c_j|\ge|i-j|$ . Here $|x|$ means the absolute value of $x$ .

However, Nauuo discovered that sometimes she couldn't find a solution because the chessboard was too small.

She wants to find the smallest chessboard on which she can put $n$ pieces according to the rules.

She also wonders how to place the pieces on such a chessboard. Can you help her?

The only line contains a single integer $n$ ( $1\le n\le 1000$ ) — the number of chess pieces for the game.

The first line contains a single integer — the minimum value of $m$ , where $m$ is the length of sides of the suitable chessboard.

The $i$ -th of the next $n$ lines contains two integers $r_i$ and $c_i$ ( $1\le r_i,c_i\le m$ ) — the coordinates of the $i$ -th chess piece.

If there are multiple answers, print any.

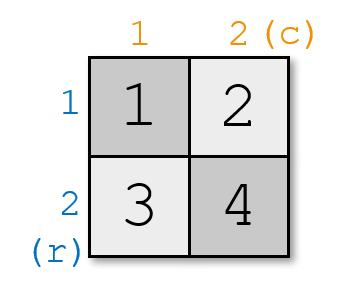
In the first example, you can't place the two pieces on a $1\times1$ chessboard without breaking the rule. But you can place two pieces on a $2\times2$ chessboard like this:

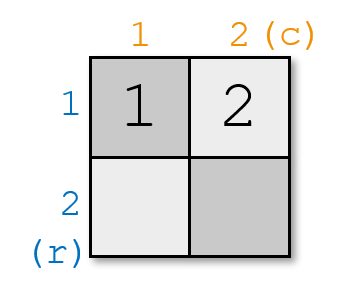
In the second example, you can't place four pieces on a $2\times2$ chessboard without breaking the rule. For example, if you place the pieces like this:

then $|r_1-r_3|+|c_1-c_3|=|1-2|+|1-1|=1$ , $|1-3|=2$ , $1<2$ ; and $|r_1-r_4|+|c_1-c_4|=|1-2|+|1-2|=2$ , $|1-4|=3$ , $2<3$ . It doesn't satisfy the rule.

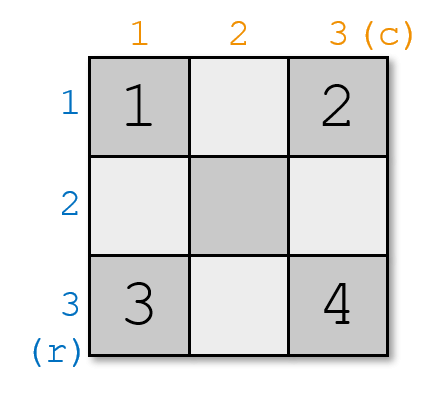
However, on a $3\times3$ chessboard, you can place four pieces like this: