CF1178D.Prime Graph

Every person likes prime numbers. Alice is a person, thus she also shares the love for them. Bob wanted to give her an affectionate gift but couldn't think of anything inventive. Hence, he will be giving her a graph. How original, Bob! Alice will surely be thrilled!

When building the graph, he needs four conditions to be satisfied:

• It must be a simple undirected graph, i.e. without multiple (parallel) edges and self-loops.
• The number of vertices must be exactly $n$ — a number he selected. This number is not necessarily prime.
• The total number of edges must be prime.
• The degree (i.e. the number of edges connected to the vertex) of each vertex must be prime.

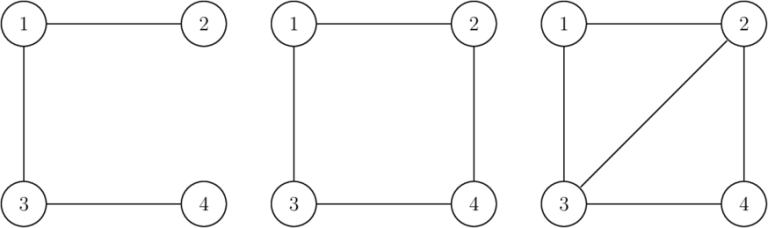
Below is an example for $n = 4$ . The first graph (left one) is invalid as the degree of vertex $2$ (and $4$ ) equals to $1$ , which is not prime. The second graph (middle one) is invalid as the total number of edges is $4$ , which is not a prime number. The third graph (right one) is a valid answer for $n = 4$ .

Note that the graph can be disconnected.

Please help Bob to find any such graph!

The input consists of a single integer $n$ ( $3 \leq n \leq 1\,000$ ) — the number of vertices.

If there is no graph satisfying the conditions, print a single line containing the integer $-1$ .

Otherwise, first print a line containing a prime number $m$ ( $2 \leq m \leq \frac{n(n-1)}{2}$ ) — the number of edges in the graph. Then, print $m$ lines, the $i$ -th of which containing two integers $u_i$ , $v_i$ ( $1 \leq u_i, v_i \leq n$ ) — meaning that there is an edge between vertices $u_i$ and $v_i$ . The degree of each vertex must be prime. There must be no multiple (parallel) edges or self-loops.

If there are multiple solutions, you may print any of them.

Note that the graph can be disconnected.

The first example was described in the statement.

In the second example, the degrees of vertices are $[7, 5, 2, 2, 3, 2, 2, 3]$ . Each of these numbers is prime. Additionally, the number of edges, $13$ , is also a prime number, hence both conditions are satisfied.