CF1140G.Double Tree

You are given a special undirected graph. It consists of $2n$ vertices numbered from $1$ to $2n$ . The following properties hold for the graph:

• there are exactly $3n-2$ edges in the graph: $n$ edges connect vertices having odd numbers with vertices having even numbers, $n - 1$ edges connect vertices having odd numbers with each other, and $n - 1$ edges connect vertices having even numbers with each other;
• for each edge $(u, v)$ between a pair of vertices with odd numbers, there exists an edge $(u + 1, v + 1)$ , and vice versa;
• for each odd number $u \in [1, 2n - 1]$ , there exists an edge $(u, u + 1)$ ;
• the graph is connected; moreover, if we delete all vertices with even numbers from it, and all edges incident to them, the graph will become a tree (the same applies to deleting odd vertices).

So, the graph can be represented as two trees having the same structure, and $n$ edges connecting each vertex of the first tree to the corresponding vertex of the second tree.

Edges of the graph are weighted. The length of some simple path in the graph is the sum of weights of traversed edges.

You are given $q$ queries to this graph; in each query, you are asked to compute the length of the shortest path between some pair of vertices in this graph. Can you answer all of the queries?

The first line of the input contains one integer $n$ ( $2 \le n \le 3 \cdot 10^5$ ).

The second line contains $n$ integers $w_{1, 2}$ , $w_{3,4}$ , ..., $w_{2n - 1, 2n}$ ( $1 \le w_{i, i + 1} \le 10^{12}$ ). These integers describe the weights of the edges connecting odd vertices with even ones.

Then $n-1$ lines follow. $i$ -th line contains four integers $x_i$ , $y_i$ , $w_{i, 1}$ and $w_{i, 2}$ ( $1 \le x_i, y_i \le n$ , $x_i \ne y_i$ , $1 \le w_{i, j} \le 10^{12}$ ); it describes two edges: one connecting $2x_i - 1$ with $2y_i - 1$ and having weight $w_{i, 1}$ ; another connecting $2x_i$ with $2y_i$ and having weight $w_{i, 2}$ .

The next line contains one integer $q$ ( $1 \le q \le 6 \cdot 10^5$ ) — the number of queries.

Then $q$ lines follow, $i$ -th line contains two integers $u_i$ and $v_i$ ( $1 \le u_i, v_i \le 2n$ , $u_i \ne v_i$ ), describing a query "compute the length of the shortest path between vertices $u_i$ and $v_i$ ".

Print $q$ integers, $i$ -th integer should be equal to the answer to the $i$ -th query.

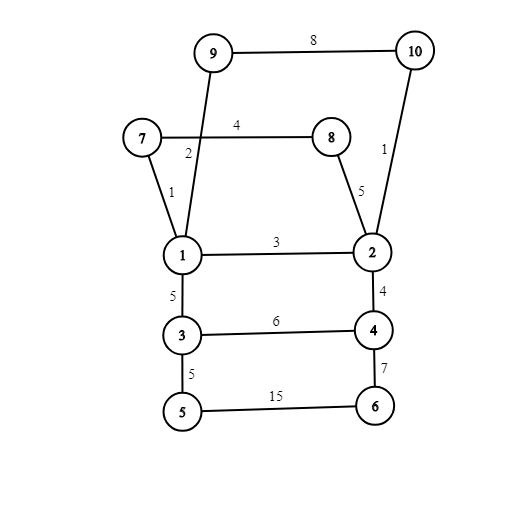
The graph in the first test looks like that: