CF1146H.Satanic Panic

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

You are given a set of $n$ points in a 2D plane. No three points are collinear.

A pentagram is a set of $5$ points $A,B,C,D,E$ that can be arranged as follows. 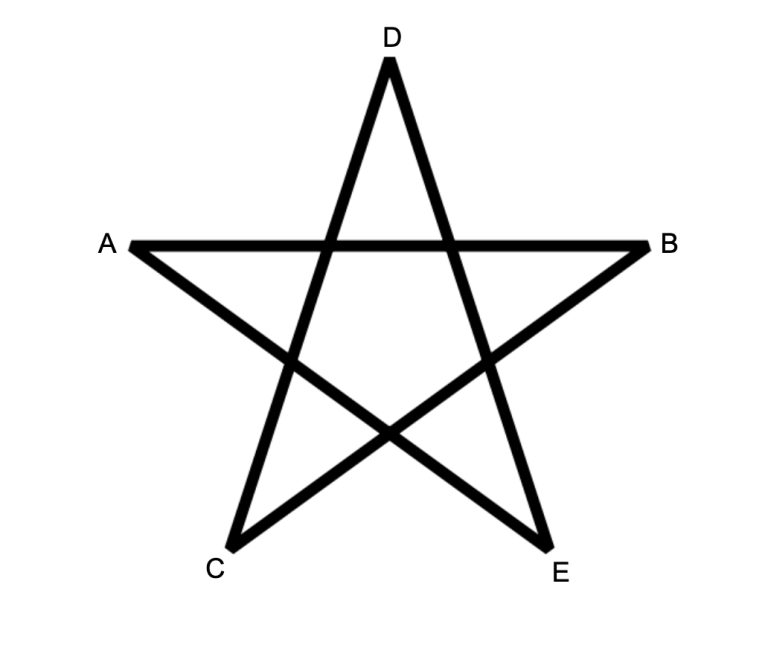Note the length of the line segments don't matter, only that those particular intersections exist.

Count the number of ways to choose $5$ points from the given set that form a pentagram.

输入格式

The first line contains an integer $n$ ( $5 \leq n \leq 300$ ) — the number of points.

Each of the next $n$ lines contains two integers $x_i, y_i$ ( $-10^6 \leq x_i,y_i \leq 10^6$ ) — the coordinates of the $i$ -th point. It is guaranteed that no three points are collinear.

输出格式

Print a single integer, the number of sets of $5$ points that form a pentagram.

输入输出样例

输入#1
```
5
0 0
0 2
2 0
2 2
1 3
```
输出#1
```
1
```
输入#2
```
5
0 0
4 0
0 4
4 4
2 3
```
输出#2
```
0
```

输入#3

10
841746 527518
595261 331297
-946901 129987
670374 -140388
-684770 309555
-302589 415564
-387435 613331
-624940 -95922
945847 -199224
24636 -565799

输出#3

说明/提示

A picture of the first sample: A picture of the second sample: A picture of the third sample:

首页