CF1130C.Connect

Alice lives on a flat planet that can be modeled as a square grid of size $n \times n$ , with rows and columns enumerated from $1$ to $n$ . We represent the cell at the intersection of row $r$ and column $c$ with ordered pair $(r, c)$ . Each cell in the grid is either land or water.

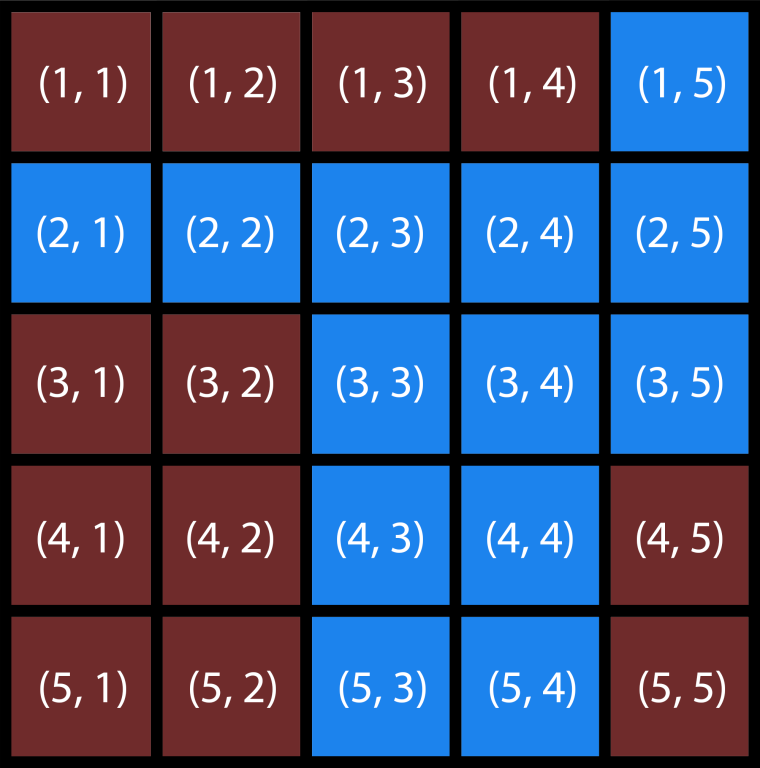An example planet with $n = 5$ . It also appears in the first sample test.Alice resides in land cell $(r_1, c_1)$ . She wishes to travel to land cell $(r_2, c_2)$ . At any moment, she may move to one of the cells adjacent to where she is—in one of the four directions (i.e., up, down, left, or right).

Unfortunately, Alice cannot swim, and there is no viable transportation means other than by foot (i.e., she can walk only on land). As a result, Alice's trip may be impossible.

To help Alice, you plan to create at most one tunnel between some two land cells. The tunnel will allow Alice to freely travel between the two endpoints. Indeed, creating a tunnel is a lot of effort: the cost of creating a tunnel between cells $(r_s, c_s)$ and $(r_t, c_t)$ is $(r_s-r_t)^2 + (c_s-c_t)^2$ .

For now, your task is to find the minimum possible cost of creating at most one tunnel so that Alice could travel from $(r_1, c_1)$ to $(r_2, c_2)$ . If no tunnel needs to be created, the cost is $0$ .

The first line contains one integer $n$ ( $1 \leq n \leq 50$ ) — the width of the square grid.

The second line contains two space-separated integers $r_1$ and $c_1$ ( $1 \leq r_1, c_1 \leq n$ ) — denoting the cell where Alice resides.

The third line contains two space-separated integers $r_2$ and $c_2$ ( $1 \leq r_2, c_2 \leq n$ ) — denoting the cell to which Alice wishes to travel.

Each of the following $n$ lines contains a string of $n$ characters. The $j$ -th character of the $i$ -th such line ( $1 \leq i, j \leq n$ ) is 0 if $(i, j)$ is land or 1 if $(i, j)$ is water.

It is guaranteed that $(r_1, c_1)$ and $(r_2, c_2)$ are land.

Print an integer that is the minimum possible cost of creating at most one tunnel so that Alice could travel from $(r_1, c_1)$ to $(r_2, c_2)$ .

In the first sample, a tunnel between cells $(1, 4)$ and $(4, 5)$ should be created. The cost of doing so is $(1-4)^2 + (4-5)^2 = 10$ , which is optimal. This way, Alice could walk from $(1, 1)$ to $(1, 4)$ , use the tunnel from $(1, 4)$ to $(4, 5)$ , and lastly walk from $(4, 5)$ to $(5, 5)$ .

In the second sample, clearly a tunnel between cells $(1, 3)$ and $(3, 1)$ needs to be created. The cost of doing so is $(1-3)^2 + (3-1)^2 = 8$ .