CF1133F2.Spanning Tree with One Fixed Degree

You are given an undirected unweighted connected graph consisting of $n$ vertices and $m$ edges. It is guaranteed that there are no self-loops or multiple edges in the given graph.

Your task is to find any spanning tree of this graph such that the degree of the first vertex (vertex with label $1$ on it) is equal to $D$ (or say that there are no such spanning trees). Recall that the degree of a vertex is the number of edges incident to it.

The first line contains three integers $n$ , $m$ and $D$ ( $2 \le n \le 2 \cdot 10^5$ , $n - 1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2}), 1 \le D < n$ ) — the number of vertices, the number of edges and required degree of the first vertex, respectively.

The following $m$ lines denote edges: edge $i$ is represented by a pair of integers $v_i$ , $u_i$ ( $1 \le v_i, u_i \le n$ , $u_i \ne v_i$ ), which are the indices of vertices connected by the edge. There are no loops or multiple edges in the given graph, i. e. for each pair ( $v_i, u_i$ ) there are no other pairs ( $v_i, u_i$ ) or ( $u_i, v_i$ ) in the list of edges, and for each pair $(v_i, u_i)$ the condition $v_i \ne u_i$ is satisfied.

If there is no spanning tree satisfying the condition from the problem statement, print "NO" in the first line.

Otherwise print "YES" in the first line and then print $n-1$ lines describing the edges of a spanning tree such that the degree of the first vertex (vertex with label $1$ on it) is equal to $D$ . Make sure that the edges of the printed spanning tree form some subset of the input edges (order doesn't matter and edge $(v, u)$ is considered the same as the edge $(u, v)$ ).

If there are multiple possible answers, print any of them.

The picture corresponding to the first and second examples: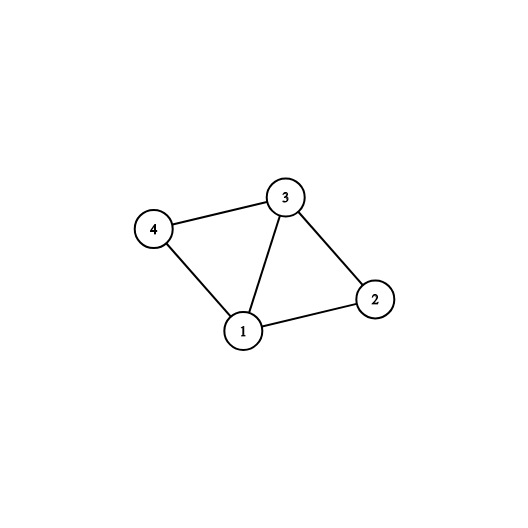

The picture corresponding to the third example: