CF1139C.Edgy Trees
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You are given a tree (a connected undirected graph without cycles) of n vertices. Each of the n−1 edges of the tree is colored in either black or red.
You are also given an integer k . Consider sequences of k vertices. Let's call a sequence [a1,a2,…,ak] good if it satisfies the following criterion:
- We will walk a path (possibly visiting same edge/vertex multiple times) on the tree, starting from a1 and ending at ak .
- Start at a1 , then go to a2 using the shortest path between a1 and a2 , then go to a3 in a similar way, and so on, until you travel the shortest path between ak−1 and ak .
- If you walked over at least one black edge during this process, then the sequence is good.
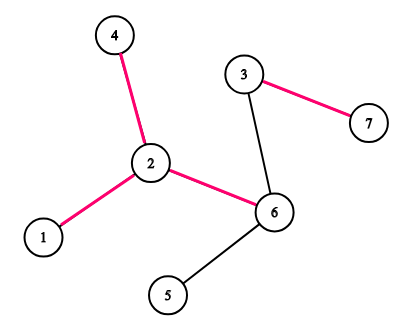 Consider the tree on the picture. If k=3 then the following sequences are good: [1,4,7] , [5,5,3] and [2,3,7] . The following sequences are not good: [1,4,6] , [5,5,5] , [3,7,3] .
Consider the tree on the picture. If k=3 then the following sequences are good: [1,4,7] , [5,5,3] and [2,3,7] . The following sequences are not good: [1,4,6] , [5,5,5] , [3,7,3] .
There are nk sequences of vertices, count how many of them are good. Since this number can be quite large, print it modulo 109+7 .
输入格式
The first line contains two integers n and k ( 2≤n≤105 , 2≤k≤100 ), the size of the tree and the length of the vertex sequence.
Each of the next n−1 lines contains three integers ui , vi and xi ( 1≤ui,vi≤n , xi∈{0,1} ), where ui and vi denote the endpoints of the corresponding edge and xi is the color of this edge ( 0 denotes red edge and 1 denotes black edge).
输出格式
Print the number of good sequences modulo 109+7 .
输入输出样例
输入#1
4 4 1 2 1 2 3 1 3 4 1
输出#1
252
输入#2
4 6 1 2 0 1 3 0 1 4 0
输出#2
0
输入#3
3 5 1 2 1 2 3 0
输出#3
210
说明/提示
In the first example, all sequences ( 44 ) of length 4 except the following are good:
- [1,1,1,1]
- [2,2,2,2]
- [3,3,3,3]
- [4,4,4,4]
In the second example, all edges are red, hence there aren't any good sequences.