CF1067B.Multihedgehog

Someone give a strange birthday present to Ivan. It is hedgehog — connected undirected graph in which one vertex has degree at least $3$ (we will call it center) and all other vertices has degree 1. Ivan thought that hedgehog is too boring and decided to make himself $k$ -multihedgehog.

Let us define $k$ -multihedgehog as follows:

• $1$ -multihedgehog is hedgehog: it has one vertex of degree at least $3$ and some vertices of degree 1.
• For all $k \ge 2$ , $k$ -multihedgehog is $(k-1)$ -multihedgehog in which the following changes has been made for each vertex $v$ with degree 1: let $u$ be its only neighbor; remove vertex $v$ , create a new hedgehog with center at vertex $w$ and connect vertices $u$ and $w$ with an edge. New hedgehogs can differ from each other and the initial gift.

Thereby $k$ -multihedgehog is a tree. Ivan made $k$ -multihedgehog but he is not sure that he did not make any mistakes. That is why he asked you to check if his tree is indeed $k$ -multihedgehog.

First line of input contains $2$ integers $n$ , $k$ ( $1 \le n \le 10^{5}$ , $1 \le k \le 10^{9}$ ) — number of vertices and hedgehog parameter.

Next $n-1$ lines contains two integers $u$ $v$ ( $1 \le u, \,\, v \le n; \,\, u \ne v$ ) — indices of vertices connected by edge.

It is guaranteed that given graph is a tree.

Print "Yes" (without quotes), if given graph is $k$ -multihedgehog, and "No" (without quotes) otherwise.

2-multihedgehog from the first example looks like this:

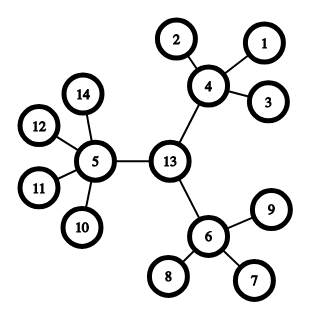
Its center is vertex $13$ . Hedgehogs created on last step are: [4 (center), 1, 2, 3], [6 (center), 7, 8, 9], [5 (center), 10, 11, 12, 13].

Tree from second example is not a hedgehog because degree of center should be at least $3$ .