CF1083A.The Fair Nut and the Best Path
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
The Fair Nut is going to travel to the Tree Country, in which there are n cities. Most of the land of this country is covered by forest. Furthermore, the local road system forms a tree (connected graph without cycles). Nut wants to rent a car in the city u and go by a simple path to city v . He hasn't determined the path, so it's time to do it. Note that chosen path can consist of only one vertex.
A filling station is located in every city. Because of strange law, Nut can buy only wi liters of gasoline in the i -th city. We can assume, that he has infinite money. Each road has a length, and as soon as Nut drives through this road, the amount of gasoline decreases by length. Of course, Nut can't choose a path, which consists of roads, where he runs out of gasoline. He can buy gasoline in every visited city, even in the first and the last.
He also wants to find the maximum amount of gasoline that he can have at the end of the path. Help him: count it.
输入格式
The first line contains a single integer n ( 1≤n≤3⋅105 ) — the number of cities.
The second line contains n integers w1,w2,…,wn ( 0≤wi≤109 ) — the maximum amounts of liters of gasoline that Nut can buy in cities.
Each of the next n−1 lines describes road and contains three integers u , v , c ( 1≤u,v≤n , 1≤c≤109 , u=v ), where u and v — cities that are connected by this road and c — its length.
It is guaranteed that graph of road connectivity is a tree.
输出格式
Print one number — the maximum amount of gasoline that he can have at the end of the path.
输入输出样例
输入#1
3 1 3 3 1 2 2 1 3 2
输出#1
3
输入#2
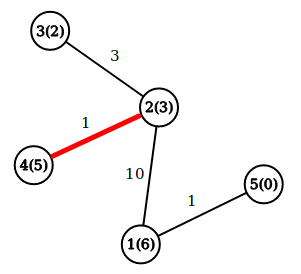
5 6 3 2 5 0 1 2 10 2 3 3 2 4 1 1 5 1
输出#2
7
说明/提示
The optimal way in the first example is 2→1→3 .
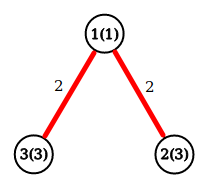 The optimal way in the second example is 2→4 .
The optimal way in the second example is 2→4 .