CF1085D.Minimum Diameter Tree
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You are given a tree (an undirected connected graph without cycles) and an integer s .
Vanya wants to put weights on all edges of the tree so that all weights are non-negative real numbers and their sum is s . At the same time, he wants to make the diameter of the tree as small as possible.
Let's define the diameter of a weighed tree as the maximum sum of the weights of the edges lying on the path between two some vertices of the tree. In other words, the diameter of a weighed tree is the length of the longest simple path in the tree, where length of a path is equal to the sum of weights over all edges in the path.
Find the minimum possible diameter that Vanya can get.
输入格式
The first line contains two integer numbers n and s ( 2≤n≤105 , 1≤s≤109 ) — the number of vertices in the tree and the sum of edge weights.
Each of the following n−1 lines contains two space-separated integer numbers ai and bi ( 1≤ai,bi≤n , ai=bi ) — the indexes of vertices connected by an edge. The edges are undirected.
It is guaranteed that the given edges form a tree.
输出格式
Print the minimum diameter of the tree that Vanya can get by placing some non-negative real weights on its edges with the sum equal to s .
Your answer will be considered correct if its absolute or relative error does not exceed 10−6 .
Formally, let your answer be a , and the jury's answer be b . Your answer is considered correct if max(1,b)∣a−b∣≤10−6 .
输入输出样例
输入#1
4 3 1 2 1 3 1 4
输出#1
2.000000000000000000
输入#2
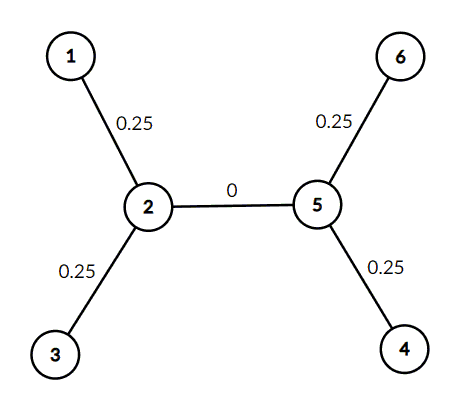
6 1 2 1 2 3 2 5 5 4 5 6
输出#2
0.500000000000000000
输入#3
5 5 1 2 2 3 3 4 3 5
输出#3
3.333333333333333333
说明/提示
In the first example it is necessary to put weights like this:
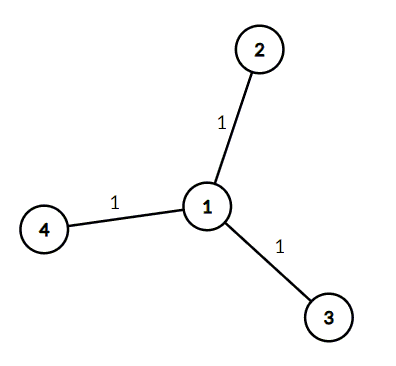 It is easy to see that the diameter of this tree is 2 . It can be proved that it is the minimum possible diameter.
It is easy to see that the diameter of this tree is 2 . It can be proved that it is the minimum possible diameter.
In the second example it is necessary to put weights like this: