CF1044B.Intersecting Subtrees

You are playing a strange game with Li Chen. You have a tree with $n$ nodes drawn on a piece of paper. All nodes are unlabeled and distinguishable. Each of you independently labeled the vertices from $1$ to $n$ . Neither of you know the other's labelling of the tree.

You and Li Chen each chose a subtree (i.e., a connected subgraph) in that tree. Your subtree consists of the vertices labeled $x_1, x_2, \ldots, x_{k_1}$ in your labeling, Li Chen's subtree consists of the vertices labeled $y_1, y_2, \ldots, y_{k_2}$ in his labeling. The values of $x_1, x_2, \ldots, x_{k_1}$ and $y_1, y_2, \ldots, y_{k_2}$ are known to both of you.

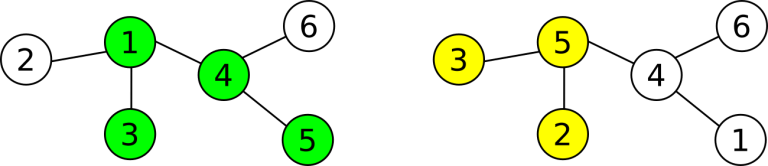The picture shows two labelings of a possible tree: yours on the left and Li Chen's on the right. The selected trees are highlighted. There are two common nodes.You want to determine whether your subtrees have at least one common vertex. Luckily, your friend Andrew knows both labelings of the tree. You can ask Andrew at most $5$ questions, each of which is in one of the following two forms:

• A x: Andrew will look at vertex $x$ in your labeling and tell you the number of this vertex in Li Chen's labeling.
• B y: Andrew will look at vertex $y$ in Li Chen's labeling and tell you the number of this vertex in your labeling.

Determine whether the two subtrees have at least one common vertex after asking some questions. If there is at least one common vertex, determine one of your labels for any of the common vertices.

无

Each test consists of several test cases.

The first line of input contains a single integer $t$ ( $1 \leq t \leq 100$ ) — the number of test cases.

For each testcase, your program should interact in the following format.

The first line contains a single integer $n$ ( $1 \leq n \leq 1\,000$ ) — the number of nodes in the tree.

Each of the next $n-1$ lines contains two integers $a_i$ and $b_i$ ( $1\leq a_i, b_i\leq n$ ) — the edges of the tree, indicating an edge between node $a_i$ and $b_i$ according to your labeling of the nodes.

The next line contains a single integer $k_1$ ( $1 \leq k_1 \leq n$ ) — the number of nodes in your subtree.

The next line contains $k_1$ distinct integers $x_1,x_2,\ldots,x_{k_1}$ ( $1 \leq x_i \leq n$ ) — the indices of the nodes in your subtree, according to your labeling. It is guaranteed that these vertices form a subtree.

The next line contains a single integer $k_2$ ( $1 \leq k_2 \leq n$ ) — the number of nodes in Li Chen's subtree.

The next line contains $k_2$ distinct integers $y_1, y_2, \ldots, y_{k_2}$ ( $1 \leq y_i \leq n$ ) — the indices (according to Li Chen's labeling) of the nodes in Li Chen's subtree. It is guaranteed that these vertices form a subtree according to Li Chen's labelling of the tree's nodes.

Test cases will be provided one by one, so you must complete interacting with the previous test (i.e. by printing out a common node or $-1$ if there is not such node) to start receiving the next one.

You can ask the Andrew two different types of questions.

• You can print "A x" ( $1 \leq x \leq n$ ). Andrew will look at vertex $x$ in your labeling and respond to you with the number of this vertex in Li Chen's labeling.
• You can print "B y" ( $1 \leq y \leq n$ ). Andrew will look at vertex $y$ in Li Chen's labeling and respond to you with the number of this vertex in your labeling.

You may only ask at most $5$ questions per tree.

When you are ready to answer, print "C s", where $s$ is your label of a vertex that is common to both subtrees, or $-1$ , if no such vertex exists. Printing the answer does not count as a question. Remember to flush your answer to start receiving the next test case.

After printing a question do not forget to print end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:

• fflush(stdout) or cout.flush() in C++;
• System.out.flush() in Java;
• flush(output) in Pascal;
• stdout.flush() in Python;
• see documentation for other languages.

If the judge responds with $-1$ , it means that you asked more queries than allowed, or asked an invalid query. Your program should immediately terminate (for example, by calling exit(0)). You will receive Wrong Answer; it means that you asked more queries than allowed, or asked an invalid query. If you ignore this, you can get other verdicts since your program will continue to read from a closed stream.

Hack Format

To hack, use the following format. Note that you can only hack with one test case.

The first line should contain a single integer $t$ ( $t=1$ ).

The second line should contain a single integer $n$ ( $1 \leq n \leq 1\,000$ ).

The third line should contain $n$ integers $p_1, p_2, \ldots, p_n$ ( $1\leq p_i\leq n$ ) — a permutation of $1$ to $n$ . This encodes the labels that Li Chen chose for his tree. In particular, Li Chen chose label $p_i$ for the node you labeled $i$ .

Each of the next $n-1$ lines should contain two integers $a_i$ and $b_i$ ( $1\leq a_i, b_i\leq n$ ). These edges should form a tree.

The next line should contain a single integer $k_1$ ( $1 \leq k_1 \leq n$ ).

The next line should contain $k_1$ distinct integers $x_1,x_2,\ldots,x_{k_1}$ ( $1 \leq x_i \leq n$ ). These vertices should form a subtree.

The next line should contain a single integer $k_2$ ( $1 \leq k_2 \leq n$ ).

The next line should contain $k_2$ distinct integers $y_1, y_2, \ldots, y_{k_2}$ ( $1 \leq y_i \leq n$ ). These vertices should form a subtree in Li Chen's tree according to the permutation above.

For the first sample, Li Chen's hidden permutation is $[2, 3, 1]$ , and for the second, his hidden permutation is $[5, 3, 2, 4, 1, 6]$ for both cases.

In the first sample, there is a tree with three nodes in a line. On the top, is how you labeled the tree and the subtree you chose, and the bottom is how Li Chen labeled the tree and the subtree he chose:

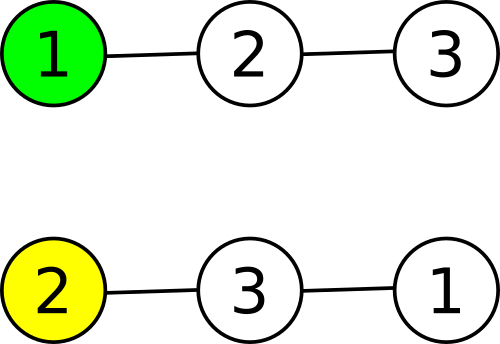In the first question, you ask Andrew to look at node $1$ in your labelling and tell you the label of it in Li Chen's labelling. Andrew responds with $2$ . At this point, you know that both of your subtrees contain the same node (i.e. node $1$ according to your labeling), so you can output "C 1" and finish. However, you can also ask Andrew to look at node $2$ in Li Chen's labelling and tell you the label of it in your labelling. Andrew responds with $1$ (this step was given with the only reason — to show you how to ask questions).

For the second sample, there are two test cases. The first looks is the one from the statement:

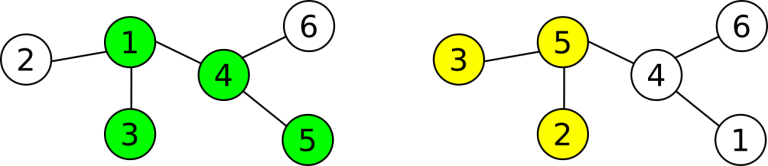We first ask "B 2", and Andrew will tell us $3$ . In this case, we know $3$ is a common vertex, and moreover, any subtree with size $3$ that contains node $3$ must contain node $1$ as well, so we can output either "C 1" or "C 3" as our answer.

In the second case in the second sample, the situation looks as follows:

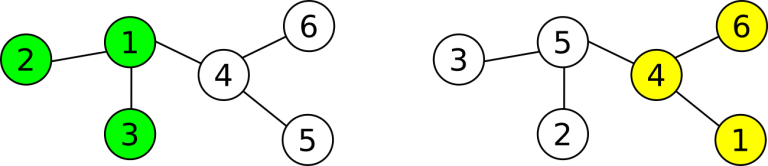In this case, you know that the only subtree of size $3$ that doesn't contain node $1$ is subtree $4,5,6$ . You ask Andrew for the label of node $1$ in Li Chen's labelling and Andrew says $5$ . In this case, you know that Li Chen's subtree doesn't contain node $1$ , so his subtree must be consist of the nodes $4,5,6$ (in your labelling), thus the two subtrees have no common nodes.