CF1044F.DFS

Let $T$ be a tree on $n$ vertices. Consider a graph $G_0$ , initially equal to $T$ . You are given a sequence of $q$ updates, where the $i$ -th update is given as a pair of two distinct integers $u_i$ and $v_i$ .

For every $i$ from $1$ to $q$ , we define the graph $G_i$ as follows:

• If $G_{i-1}$ contains an edge $\{u_i, v_i\}$ , then remove this edge to form $G_i$ .
• Otherwise, add this edge to $G_{i-1}$ to form $G_i$ .

Formally, $G_i := G_{i-1} \triangle \{\{u_i, v_i\}\}$ where $\triangle$ denotes the set symmetric difference.

Furthermore, it is guaranteed that $T$ is always a subgraph of $G_i$ . In other words, an update never removes an edge of $T$ .

Consider a connected graph $H$ and run a depth-first search on it. One can see that the tree edges (i.e. the edges leading to a not yet visited vertex at the time of traversal) form a spanning tree of the graph $H$ . This spanning tree is not generally fixed for a particular graph — it depends on the starting vertex, and on the order in which the neighbors of each vertex are traversed.

We call vertex $w$ good if one can order the neighbors of each vertex in such a way that the depth-first search started from $w$ produces $T$ as the spanning tree. For every $i$ from $1$ to $q$ , find and report the number of good vertices.

The first line contains two integers $n$ and $q$ ( $3 \le n \le 2\cdot 10^5$ , $1 \le q \le 2 \cdot 10^5$ ) — the number of nodes and the number of updates, respectively.

Each of the next $n-1$ lines contains two integers $u$ and $v$ ( $1 \le u, v \le n$ , $u \ne v$ ) — vertices connected by an edge in $T$ . It is guaranteed that this graph is a tree.

Each of the next $q$ lines contains two integers $u$ and $v$ ( $1 \le u, v \le n$ , $u \ne v$ ) — the endpoints of the edge that is added or removed. It is guaranteed that this edge does not belong to $T$ .

For each update, print one integer $k$ — the number of good vertices $w$ after the corresponding update.

The first sample is depicted in the following figure.

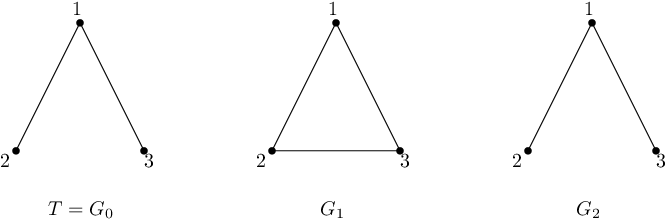After the first update, $G$ contains all three possible edges. The result of a DFS is as follows:

• Let the starting vertex be $1$ . We have two choices of ordering the neighbors of $1$ , either $[2, 3]$ or $[3, 2]$ .

  • If we choose the former, then we reach vertex $2$ . Regardless of the ordering of its neighbors, the next visited vertex will be $3$ . Thus, the spanning tree generated by this DFS will contain edges $\{1, 2\}$ and $\{2, 3\}$ , which does not equal to $T$ .
  • If we choose the latter, we obtain a spanning tree with edges $\{1, 3\}$ and $\{2, 3\}$ .

  Hence, there is no way of ordering the neighbors of vertices such that the DFS produces $T$ , and subsequently $1$ is not a good vertex.

• Let the starting vertex be $2$ . We have two choices of traversing its neighbors. If we visit $3$ first, then the spanning tree will consist of edges $\{2,3\}$ and $\{1,3\}$ , which is not equal to $T$ . If we, however, visit $1$ first, then we can only continue to $3$ from here, and the spanning tree will consist of edges $\{1, 2\}$ and $\{1,3\}$ , which equals to $T$ . Hence, $2$ is a good vertex.

• The case when we start in the vertex $3$ is symmetrical to starting in $2$ , and hence $3$ is a good vertex.

Therefore, the answer is $2$ .After the second update, the edge between $2$ and $3$ is removed, and $G = T$ . It follows that the spanning tree generated by DFS will be always equal to $T$ independent of the choice of the starting vertex. Thus, the answer is $3$ .

In the second sample, the set of good vertices after the corresponding query is:

• $\{2, 3, 5\}$
• $\{3, 5\}$
• $\{3, 4, 5\}$
• $\{4, 5\}$
• $\{4, 5, 6\}$
• $\{5, 6\}$