CF1062F.Upgrading Cities

There are $n$ cities in the kingdom $X$ , numbered from $1$ through $n$ . People travel between cities by some one-way roads. As a passenger, JATC finds it weird that from any city $u$ , he can't start a trip in it and then return back to it using the roads of the kingdom. That is, the kingdom can be viewed as an acyclic graph.

Being annoyed by the traveling system, JATC decides to meet the king and ask him to do something. In response, the king says that he will upgrade some cities to make it easier to travel. Because of the budget, the king will only upgrade those cities that are important or semi-important. A city $u$ is called important if for every city $v \neq u$ , there is either a path from $u$ to $v$ or a path from $v$ to $u$ . A city $u$ is called semi-important if it is not important and we can destroy exactly one city $v \neq u$ so that $u$ becomes important.

The king will start to act as soon as he finds out all those cities. Please help him to speed up the process.

The first line of the input contains two integers $n$ and $m$ ( $2 \le n \le 300\,000$ , $1 \le m \le 300\,000$ ) — the number of cities and the number of one-way roads.

Next $m$ lines describe the road system of the kingdom. Each of them contains two integers $u_i$ and $v_i$ ( $1 \le u_i, v_i \le n$ , $u_i \neq v_i$ ), denoting one-way road from $u_i$ to $v_i$ .

It is guaranteed, that the kingdoms' roads make an acyclic graph, which doesn't contain multiple edges and self-loops.

Print a single integer — the number of cities that the king has to upgrade.

In the first example:

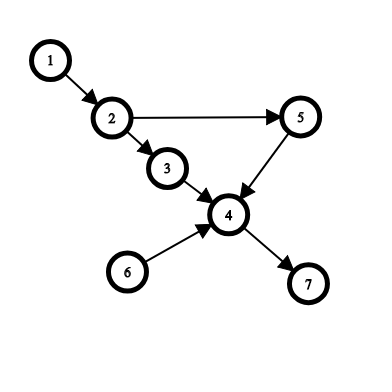- Starting at the city $1$ we can reach all the other cities, except for the city $6$ . Also, from the city $6$ we cannot reach the city $1$ . Therefore, if we destroy the city $6$ then the city $1$ will become important. So $1$ is a semi-important city.

• For city $2$ , the set of cities that cannot reach $2$ and cannot be reached by $2$ is $\{6\}$ . Therefore, destroying city $6$ will make the city $2$ important. So city $2$ is also semi-important.
• For city $3$ , the set is $\{5, 6\}$ . As you can see, destroying either city $5$ or $6$ will not make the city $3$ important. Therefore, it is neither important nor semi-important.
• For city $4$ , the set is empty. So $4$ is an important city.
• The set for city $5$ is $\{3, 6\}$ and the set for city $6$ is $\{3, 5\}$ . Similarly to city $3$ , both of them are not important nor semi-important.
• The city $7$ is important since we can reach it from all other cities.

So we have two important cities ( $4$ and $7$ ) and two semi-important cities ( $1$ and $2$ ).In the second example, the important cities are $1$ and $4$ . The semi-important cities are $2$ and $3$ .