CF1007E.Mini Metro

In a simplified version of a "Mini Metro" game, there is only one subway line, and all the trains go in the same direction. There are $n$ stations on the line, $a_i$ people are waiting for the train at the $i$ -th station at the beginning of the game. The game starts at the beginning of the $0$ -th hour. At the end of each hour (couple minutes before the end of the hour), $b_i$ people instantly arrive to the $i$ -th station. If at some moment, the number of people at the $i$ -th station is larger than $c_i$ , you lose.

A player has several trains which he can appoint to some hours. The capacity of each train is $k$ passengers. In the middle of the appointed hour, the train goes from the $1$ -st to the $n$ -th station, taking as many people at each station as it can accommodate. A train can not take people from the $i$ -th station if there are people at the $i-1$ -th station.

If multiple trains are appointed to the same hour, their capacities are being added up and they are moving together.

The player wants to stay in the game for $t$ hours. Determine the minimum number of trains he will need for it.

The first line contains three integers $n$ , $t$ , and $k$ ( $1 \leq n, t \leq 200, 1 \leq k \leq 10^9$ ) — the number of stations on the line, hours we want to survive, and capacity of each train respectively.

Each of the next $n$ lines contains three integers $a_i$ , $b_i$ , and $c_i$ ( $0 \leq a_i, b_i \leq c_i \leq 10^9$ ) — number of people at the $i$ -th station in the beginning of the game, number of people arriving to $i$ -th station in the end of each hour and maximum number of people at the $i$ -th station allowed respectively.

Output a single integer number — the answer to the problem.

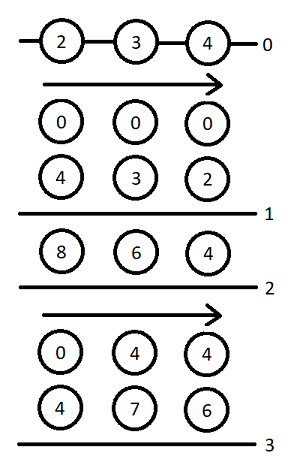
Let's look at the sample. There are three stations, on the first, there are initially 2 people, 3 people on the second, and 4 people on the third. Maximal capacities of the stations are 10, 9, and 8 respectively.

One of the winning strategies is to appoint two trains to the first and the third hours. Then on the first hour, the train takes all of the people from the stations, and at the end of the hour, 4 people arrive at the first station, 3 on the second, and 2 on the third.

In the second hour there are no trains appointed, and at the end of it, the same amount of people are arriving again.

In the third hour, the train first takes 8 people from the first station, and when it arrives at the second station, it takes only 2 people because it can accommodate no more than 10 people. Then it passes by the third station because it is already full. After it, people arrive at the stations once more, and the game ends.

As there was no such moment when the number of people at a station exceeded maximal capacity, we won using two trains.