CF985D.Sand Fortress

You are going to the beach with the idea to build the greatest sand castle ever in your head! The beach is not as three-dimensional as you could have imagined, it can be decribed as a line of spots to pile up sand pillars. Spots are numbered $1$ through infinity from left to right.

Obviously, there is not enough sand on the beach, so you brought $n$ packs of sand with you. Let height $h_{i}$ of the sand pillar on some spot $i$ be the number of sand packs you spent on it. You can't split a sand pack to multiple pillars, all the sand from it should go to a single one. There is a fence of height equal to the height of pillar with $H$ sand packs to the left of the first spot and you should prevent sand from going over it.

Finally you ended up with the following conditions to building the castle:

• $h_{1}<=H$ : no sand from the leftmost spot should go over the fence;
• For any 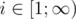$|h_{i}-h_{i+1}|<=1$ : large difference in heights of two neighboring pillars can lead sand to fall down from the higher one to the lower, you really don't want this to happen;
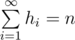• : you want to spend all the sand you brought with you.

As you have infinite spots to build, it is always possible to come up with some valid castle structure. Though you want the castle to be as compact as possible.

Your task is to calculate the minimum number of spots you can occupy so that all the aforementioned conditions hold.

The only line contains two integer numbers $n$ and $H$ ( $1<=n,H<=10^{18}$ ) — the number of sand packs you have and the height of the fence, respectively.

Print the minimum number of spots you can occupy so the all the castle building conditions hold.

Here are the heights of some valid castles:

• $n=5,H=2,[2,2,1,0,...],[2,1,1,1,0,...],[1,0,1,2,1,0,...]$
• $n=6,H=8,[3,2,1,0,...],[2,2,1,1,0,...],[0,1,0,1,2,1,1,0...]$ (this one has $5$ spots occupied)

The first list for both cases is the optimal answer, $3$ spots are occupied in them.

And here are some invalid ones:

• $n=5,H=2,[3,2,0,...],[2,3,0,...],[1,0,2,2,...]$
• $n=6,H=8,[2,2,2,0,...],[6,0,...],[1,4,1,0...],[2,2,1,0,...]$