CF989E.A Trance of Nightfall
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
The first line contains a positive integer n ( 2≤n≤200 ) — the number of points in S .
The i -th of the following n lines contains two space-separated integers xi and yi ( −104≤xi,yi≤104 ) — the coordinates of the i -th point in S . The input guarantees that for all 1≤i<j≤n , (xi,yi)=(xj,yj) holds.
The next line contains a positive integer q ( 1≤q≤200 ) — the number of queries.
Each of the following q lines contains two space-separated integers t and m ( 1≤ti≤n , 1≤mi≤104 ) — the index of the target point and the number of moves, respectively.
输入格式
Output q lines each containing a decimal number — the i -th among them denotes the maximum probability of staying on the ti -th point after mi steps, with a proper choice of starting position P .
Your answer will be considered correct if each number in your output differs from the corresponding one in jury's answer by at most 10−6 .
Formally, let your answer be a , and the jury's answer be b . Your answer is considered correct if ∣a−b∣≤10−6 .
输出格式
The points in S and possible candidates for line l are depicted in the following figure.
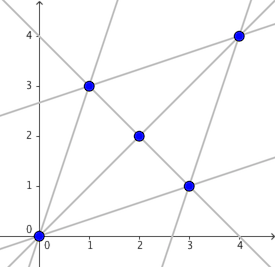 For the first query, when P=(−1,−3) , l is uniquely determined to be 3x=y , and thus Kanno will move to (0,0) with a probability of 21 .
For the first query, when P=(−1,−3) , l is uniquely determined to be 3x=y , and thus Kanno will move to (0,0) with a probability of 21 .
For the third query, when P=(2,2) , l is chosen equiprobably between x+y=4 and x=y . Kanno will then move to the other four points with a probability of 21⋅31=61 each, or stay at (2,2) with a probability of 31 .
输入输出样例
输入#1
5 0 0 1 3 2 2 3 1 4 4 10 1 1 2 1 3 1 4 1 5 1 3 2 3 3 3 4 3 5 3 6
输出#1
0.50000000000000000000 0.50000000000000000000 0.33333333333333331483 0.50000000000000000000 0.50000000000000000000 0.18518518518518517491 0.15226337448559670862 0.14494741655235482414 0.14332164812274550414 0.14296036624949901017
说明/提示
The points in S and possible candidates for line l are depicted in the following figure.
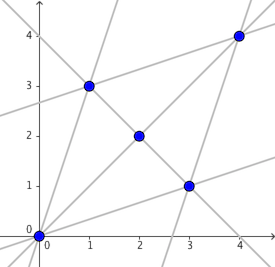 For the first query, when P=(−1,−3) , l is uniquely determined to be 3x=y , and thus Kanno will move to (0,0) with a probability of 21 .
For the first query, when P=(−1,−3) , l is uniquely determined to be 3x=y , and thus Kanno will move to (0,0) with a probability of 21 .
For the third query, when P=(2,2) , l is chosen equiprobably between x+y=4 and x=y . Kanno will then move to the other four points with a probability of 21⋅31=61 each, or stay at (2,2) with a probability of 31 .