CF997D.Cycles in product

Consider a tree (that is, an undirected connected graph without loops) $T_1$ and a tree $T_2$ . Let's define their cartesian product $T_1 \times T_2$ in a following way.

Let $V$ be the set of vertices in $T_1$ and $U$ be the set of vertices in $T_2$ .

Then the set of vertices of graph $T_1 \times T_2$ is $V \times U$ , that is, a set of ordered pairs of vertices, where the first vertex in pair is from $V$ and the second — from $U$ .

Let's draw the following edges:

• Between $(v, u_1)$ and $(v, u_2)$ there is an undirected edge, if $u_1$ and $u_2$ are adjacent in $U$ .
• Similarly, between $(v_1, u)$ and $(v_2, u)$ there is an undirected edge, if $v_1$ and $v_2$ are adjacent in $V$ .

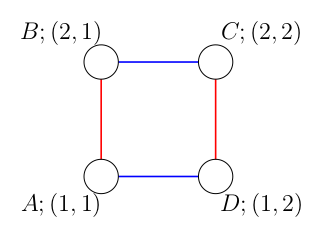
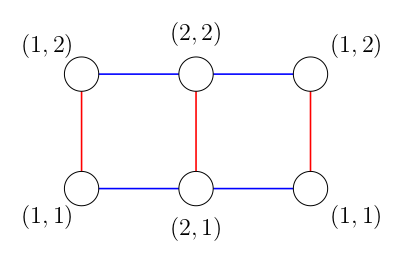
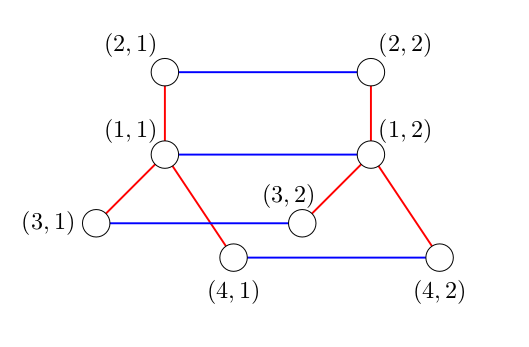
Please see the notes section for the pictures of products of trees in the sample tests.

Let's examine the graph $T_1 \times T_2$ . How much cycles (not necessarily simple) of length $k$ it contains? Since this number can be very large, print it modulo $998244353$ .

The sequence of vertices $w_1$ , $w_2$ , ..., $w_k$ , where $w_i \in V \times U$ called cycle, if any neighboring vertices are adjacent and $w_1$ is adjacent to $w_k$ . Cycles that differ only by the cyclic shift or direction of traversal are still considered different.

First line of input contains three integers — $n_1$ , $n_2$ and $k$ ( $2 \le n_1, n_2 \le 4000$ , $2 \le k \le 75$ ) — number of vertices in the first tree, number of vertices in the second tree and the cycle length respectively.

Then follow $n_1 - 1$ lines describing the first tree. Each of this lines contains two integers — $v_i, u_i$ ( $1 \le v_i, u_i \le n_1$ ), which define edges of the first tree.

Then follow $n_2 - 1$ lines, which describe the second tree in the same format.

It is guaranteed, that given graphs are trees.

Print one integer — number of cycles modulo $998244353$ .

The following three pictures illustrate graph, which are products of the trees from sample tests.

In the first example, the list of cycles of length $2$ is as follows:

• «AB», «BA»
• «BC», «CB»
• «AD», «DA»
• «CD», «DC»