CF961G.Partitions

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

You are given a set of $n$ elements indexed from $1$ to $n$ . The weight of $i$ -th element is $w_{i}$ . The weight of some subset of a given set is denoted as 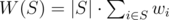. The weight of some partition $R$ of a given set into $k$ subsets is 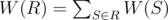(recall that a partition of a given set is a set of its subsets such that every element of the given set belongs to exactly one subset in partition).

Calculate the sum of weights of all partitions of a given set into exactly $k$ non-empty subsets, and print it modulo $10^{9}+7$ . Two partitions are considered different iff there exist two elements $x$ and $y$ such that they belong to the same set in one of the partitions, and to different sets in another partition.

输入格式

The first line contains two integers $n$ and $k$ ( $1<=k<=n<=2·10^{5}$ ) — the number of elements and the number of subsets in each partition, respectively.

The second line contains $n$ integers $w_{i}$ ( $1<=w_{i}<=10^{9}$ )— weights of elements of the set.

输出格式

Print one integer — the sum of weights of all partitions of a given set into $k$ non-empty subsets, taken modulo $10^{9}+7$ .

输入输出样例

输入#1
```
4 2
2 3 2 3
```
输出#1
```
160
```
输入#2
```
5 2
1 2 3 4 5
```
输出#2
```
645
```

说明/提示

Possible partitions in the first sample:

$\{\{1,2,3\},\{4\}\}$ , $W(R)=3\cdot(w_{1}+w_{2}+w_{3})+1\cdot w_{4}=24$ ;
$\{\{1,2,4\},\{3\}\}$ , $W(R)=26$ ;
$\{\{1,3,4\},\{2\}\}$ , $W(R)=24$ ;
$\{\{1,2\},\{3,4\}\}$ , $W(R)=2\cdot(w_{1}+w_{2})+2\cdot(w_{3}+w_{4})=20$ ;
$\{\{1,3\},\{2,4\}\}$ , $W(R)=20$ ;
$\{\{1,4\},\{2,3\}\}$ , $W(R)=20$ ;
$\{\{1\},\{2,3,4\}\}$ , $W(R)=26$ ;

Possible partitions in the second sample:

$\{\{1,2,3,4\},\{5\}\}$ , $W(R)=45$ ;
$\{\{1,2,3,5\},\{4\}\}$ , $W(R)=48$ ;
$\{\{1,2,4,5\},\{3\}\}$ , $W(R)=51$ ;
$\{\{1,3,4,5\},\{2\}\}$ , $W(R)=54$ ;
$\{\{2,3,4,5\},\{1\}\}$ , $W(R)=57$ ;
$\{\{1,2,3\},\{4,5\}\}$ , $W(R)=36$ ;
$\{\{1,2,4\},\{3,5\}\}$ , $W(R)=37$ ;
$\{\{1,2,5\},\{3,4\}\}$ , $W(R)=38$ ;
$\{\{1,3,4\},\{2,5\}\}$ , $W(R)=38$ ;
$\{\{1,3,5\},\{2,4\}\}$ , $W(R)=39$ ;
$\{\{1,4,5\},\{2,3\}\}$ , $W(R)=40$ ;
$\{\{2,3,4\},\{1,5\}\}$ , $W(R)=39$ ;
$\{\{2,3,5\},\{1,4\}\}$ , $W(R)=40$ ;
$\{\{2,4,5\},\{1,3\}\}$ , $W(R)=41$ ;
$\{\{3,4,5\},\{1,2\}\}$ , $W(R)=42$ .

首页