CF977E.Cyclic Components

You are given an undirected graph consisting of $n$ vertices and $m$ edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $a$ is connected with a vertex $b$ , a vertex $b$ is also connected with a vertex $a$ ). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices $u$ and $v$ belong to the same connected component if and only if there is at least one path along edges connecting $u$ and $v$ .

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

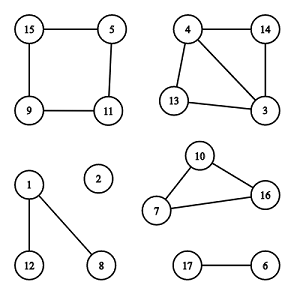There are $6$ connected components, $2$ of them are cycles: $[7, 10, 16]$ and $[5, 11, 9, 15]$ .

The first line contains two integer numbers $n$ and $m$ ( $1 \le n \le 2 \cdot 10^5$ , $0 \le m \le 2 \cdot 10^5$ ) — number of vertices and edges.

The following $m$ lines contains edges: edge $i$ is given as a pair of vertices $v_i$ , $u_i$ ( $1 \le v_i, u_i \le n$ , $u_i \ne v_i$ ). There is no multiple edges in the given graph, i.e. for each pair ( $v_i, u_i$ ) there no other pairs ( $v_i, u_i$ ) and ( $u_i, v_i$ ) in the list of edges.

Print one integer — the number of connected components which are also cycles.

In the first example only component $[3, 4, 5]$ is also a cycle.

The illustration above corresponds to the second example.