CF923C.Perfect Security

Alice has a very important message $M$ consisting of some non-negative integers that she wants to keep secret from Eve. Alice knows that the only theoretically secure cipher is one-time pad. Alice generates a random key $K$ of the length equal to the message's length. Alice computes the bitwise xor of each element of the message and the key (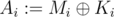, where denotes the bitwise XOR operation) and stores this encrypted message $A$ . Alice is smart. Be like Alice.

For example, Alice may have wanted to store a message $M=(0,15,9,18)$ . She generated a key $K=(16,7,6,3)$ . The encrypted message is thus $A=(16,8,15,17)$ .

Alice realised that she cannot store the key with the encrypted message. Alice sent her key $K$ to Bob and deleted her own copy. Alice is smart. Really, be like Alice.

Bob realised that the encrypted message is only secure as long as the key is secret. Bob thus randomly permuted the key before storing it. Bob thinks that this way, even if Eve gets both the encrypted message and the key, she will not be able to read the message. Bob is not smart. Don't be like Bob.

In the above example, Bob may have, for instance, selected a permutation $(3,4,1,2)$ and stored the permuted key $P=(6,3,16,7)$ .

One year has passed and Alice wants to decrypt her message. Only now Bob has realised that this is impossible. As he has permuted the key randomly, the message is lost forever. Did we mention that Bob isn't smart?

Bob wants to salvage at least some information from the message. Since he is not so smart, he asks for your help. You know the encrypted message $A$ and the permuted key $P$ . What is the lexicographically smallest message that could have resulted in the given encrypted text?

More precisely, for given $A$ and $P$ , find the lexicographically smallest message $O$ , for which there exists a permutation $π$ such that 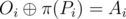for every $i$ .

Note that the sequence $S$ is lexicographically smaller than the sequence $T$ , if there is an index $i$ such that S_{i}<T_{i} and for all j<i the condition $S_{j}=T_{j}$ holds.

The first line contains a single integer $N$ ( $1<=N<=300000$ ), the length of the message.

The second line contains $N$ integers $A_{1},A_{2},...,A_{N}$ ( 0<=A_{i}<2^{30} ) representing the encrypted message.

The third line contains $N$ integers $P_{1},P_{2},...,P_{N}$ ( 0<=P_{i}<2^{30} ) representing the permuted encryption key.

Output a single line with $N$ integers, the lexicographically smallest possible message $O$ . Note that all its elements should be non-negative.

In the first case, the solution is $(10,3,28)$ , since 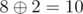, 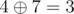and 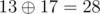. Other possible permutations of key yield messages $(25,6,10)$ , $(25,3,15)$ , $(10,21,10)$ , $(15,21,15)$ and $(15,6,28)$ , which are all lexicographically larger than the solution.