CF933E.A Preponderant Reunion

East or west, home is best. That's why family reunion, the indispensable necessity of Lunar New Year celebration, is put in such a position.

After the reunion dinner, Little Tommy plays a game with the family. Here is a concise introduction to this game:

1. There is a sequence of $n$ non-negative integers $p_{1},p_{2},...,p_{n}$ in the beginning. It is ruled that each integer in this sequence should be non-negative at any time.
2. You can select two consecutive positive integers in this sequence, $p_{i}$ and $p_{i+1}$ (1<=i<n) , and then decrease them by their minimum (i. e. $min(p_{i},p_{i+1})$ ), the cost of this operation is equal to $min(p_{i},p_{i+1})$ . We call such operation as a descension.
3. The game immediately ends when there are no two consecutive positive integers. Your task is to end the game so that the total cost of your operations is as small as possible.

Obviously, every game ends after at most $n-1$ descensions. Please share your solution of this game with the lowest cost.

The first line contains one integer $n$ $(1<=n<=3·10^{5})$ .

The second line contains $n$ space-separated integers $p_{1},p_{2},...,p_{n}$ $(0<=p_{i}<=10^{9},i=1,2,...,n)$ .

In the first line print one integer as the number of descensions $m$ $(0<=m<=n-1)$ .

In the next $m$ lines print the descensions chronologically. More precisely, in each line of the next $m$ lines print one integer $i$ (1<=i<n) representing a descension would operate on $p_{i}$ and $p_{i+1}$ such that all the descensions could be utilized from top to bottom.

If there are many possible solutions to reach the minimal cost, print any of them.

In the first sample, one possible best solution is 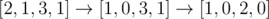, of which the cost is $1+1=2$ .

In the second sample, one possible best solution is 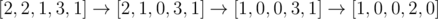, of which the cost is $1+1+1=3$ .