CF902B.Coloring a Tree

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

You are given a rooted tree with $n$ vertices. The vertices are numbered from $1$ to $n$ , the root is the vertex number $1$ .

Each vertex has a color, let's denote the color of vertex $v$ by $c_{v}$ . Initially $c_{v}=0$ .

You have to color the tree into the given colors using the smallest possible number of steps. On each step you can choose a vertex $v$ and a color $x$ , and then color all vectices in the subtree of $v$ (including $v$ itself) in color $x$ . In other words, for every vertex $u$ , such that the path from root to $u$ passes through $v$ , set $c_{u}=x$ .

It is guaranteed that you have to color each vertex in a color different from $0$ .

You can learn what a rooted tree is using the link: https://en.wikipedia.org/wiki/Tree_(graph_theory).

输入格式

The first line contains a single integer $n$ ( $2<=n<=10^{4}$ ) — the number of vertices in the tree.

The second line contains $n-1$ integers $p_{2},p_{3},...,p_{n}$ ( $1<=p_{i}<i$ ), where $p_{i}$ means that there is an edge between vertices $i$ and $p_{i}$ .

The third line contains $n$ integers $c_{1},c_{2},...,c_{n}$ ( $1<=c_{i}<=n$ ), where $c_{i}$ is the color you should color the $i$ -th vertex into.

It is guaranteed that the given graph is a tree.

输出格式

Print a single integer — the minimum number of steps you have to perform to color the tree into given colors.

输入输出样例

输入#1
```
6
1 2 2 1 5
2 1 1 1 1 1
```
输出#1
```
3
```
输入#2
```
7
1 1 2 3 1 4
3 3 1 1 1 2 3
```
输出#2
```
5
```

说明/提示

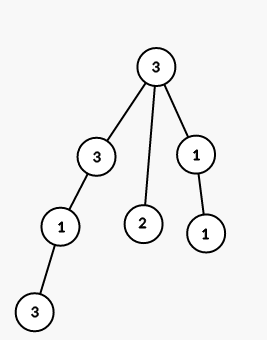
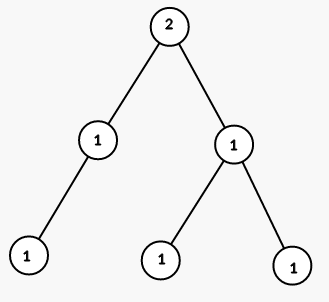
The tree from the first sample is shown on the picture (numbers are vetices' indices):

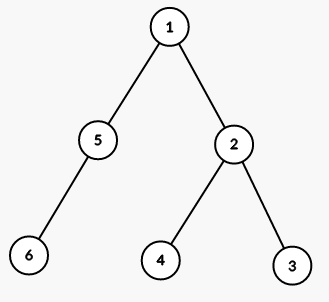
On first step we color all vertices in the subtree of vertex $1$ into color $2$ (numbers are colors):

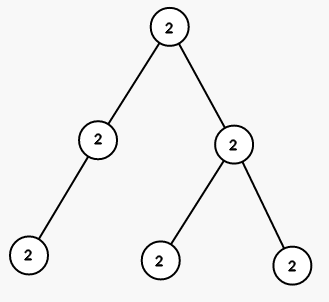
On seond step we color all vertices in the subtree of vertex $5$ into color $1$ :

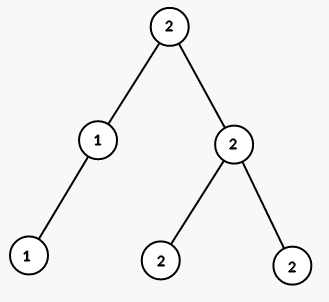
On third step we color all vertices in the subtree of vertex $2$ into color $1$ :

The tree from the second sample is shown on the picture (numbers are vetices' indices):

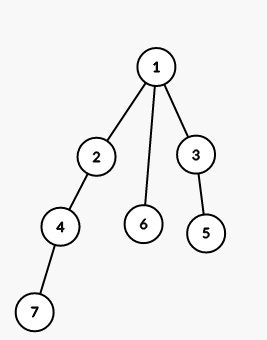
On first step we color all vertices in the subtree of vertex $1$ into color $3$ (numbers are colors):

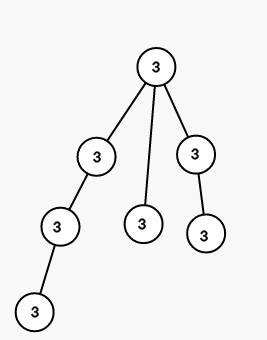
On second step we color all vertices in the subtree of vertex $3$ into color $1$ :

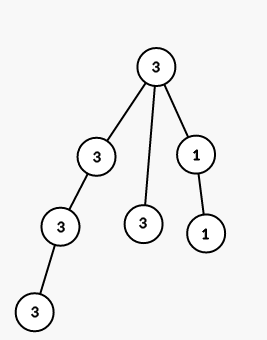
On third step we color all vertices in the subtree of vertex $6$ into color $2$ :

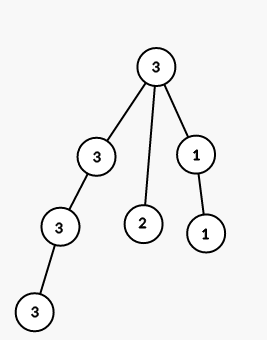
On fourth step we color all vertices in the subtree of vertex $4$ into color $1$ :

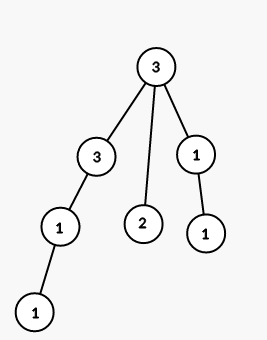
On fith step we color all vertices in the subtree of vertex $7$ into color $3$ :

首页