CF903G.Yet Another Maxflow Problem

In this problem you will have to deal with a very special network.

The network consists of two parts: part $A$ and part $B$ . Each part consists of $n$ vertices; $i$ -th vertex of part $A$ is denoted as $A_{i}$ , and $i$ -th vertex of part $B$ is denoted as $B_{i}$ .

For each index $i$ ( $1<=i<n$ ) there is a directed edge from vertex $A_{i}$ to vertex $A_{i+1}$ , and from $B_{i}$ to $B_{i+1}$ , respectively. Capacities of these edges are given in the input. Also there might be several directed edges going from part $A$ to part $B$ (but never from $B$ to $A$ ).

You have to calculate the maximum flow value from $A_{1}$ to $B_{n}$ in this network. Capacities of edges connecting $A_{i}$ to $A_{i+1}$ might sometimes change, and you also have to maintain the maximum flow value after these changes. Apart from that, the network is fixed (there are no changes in part $B$ , no changes of edges going from $A$ to $B$ , and no edge insertions or deletions).

Take a look at the example and the notes to understand the structure of the network better.

The first line contains three integer numbers $n$ , $m$ and $q$ ( $2<=n,m<=2·10^{5}$ , $0<=q<=2·10^{5}$ ) — the number of vertices in each part, the number of edges going from $A$ to $B$ and the number of changes, respectively.

Then $n-1$ lines follow, $i$ -th line contains two integers $x_{i}$ and $y_{i}$ denoting that the edge from $A_{i}$ to $A_{i+1}$ has capacity $x_{i}$ and the edge from $B_{i}$ to $B_{i+1}$ has capacity $y_{i}$ ( $1<=x_{i},y_{i}<=10^{9}$ ).

Then $m$ lines follow, describing the edges from $A$ to $B$ . Each line contains three integers $x$ , $y$ and $z$ denoting an edge from $A_{x}$ to $B_{y}$ with capacity $z$ ( $1<=x,y<=n$ , $1<=z<=10^{9}$ ). There might be multiple edges from $A_{x}$ to $B_{y}$ .

And then $q$ lines follow, describing a sequence of changes to the network. $i$ -th line contains two integers $v_{i}$ and $w_{i}$ , denoting that the capacity of the edge from $A_{vi}$ to $A_{vi}+1$ is set to $w_{i}$ ( $1<=v_{i}<n$ , $1<=w_{i}<=10^{9}$ ).

Firstly, print the maximum flow value in the original network. Then print $q$ integers, $i$ -th of them must be equal to the maximum flow value after $i$ -th change.

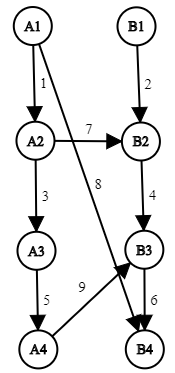
This is the original network in the example: