CF908D.New Year and Arbitrary Arrangement
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You are given three integers k , pa and pb .
You will construct a sequence with the following algorithm: Initially, start with the empty sequence. Each second, you do the following. With probability pa/(pa+pb) , add 'a' to the end of the sequence. Otherwise (with probability pb/(pa+pb) ), add 'b' to the end of the sequence.
You stop once there are at least k subsequences that form 'ab'. Determine the expected number of times 'ab' is a subsequence in the resulting sequence. It can be shown that this can be represented by P/Q , where P and Q are coprime integers, and 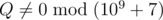 . Print the value of
. Print the value of 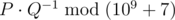 .
.
输入格式
The first line will contain three integers integer k,pa,pb ( 1<=k<=1000 , 1<=pa,pb<=1000000 ).
输出格式
Print a single integer, the answer to the problem.
输入输出样例
输入#1
1 1 1
输出#1
2
输入#2
3 1 4
输出#2
370000006
说明/提示
The first sample, we will keep appending to our sequence until we get the subsequence 'ab' at least once. For instance, we get the sequence 'ab' with probability 1/4, 'bbab' with probability 1/16, and 'aab' with probability 1/8. Note, it's impossible for us to end with a sequence like 'aabab', since we would have stopped our algorithm once we had the prefix 'aab'.
The expected amount of times that 'ab' will occur across all valid sequences is 2.
For the second sample, the answer is equal to 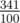 .
.