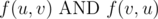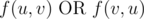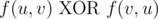CF908H.New Year and Boolean Bridges

Your friend has a hidden directed graph with $n$ nodes.

Let $f(u,v)$ be true if there is a directed path from node $u$ to node $v$ , and false otherwise. For each pair of distinct nodes, $u,v$ , you know at least one of the three statements is true:

1. 
2. 
3. 

Here AND, OR and XOR mean AND, OR and exclusive OR operations, respectively.

You are given an $n$ by $n$ matrix saying which one of the three statements holds for each pair of vertices. The entry in the $u$ -th row and $v$ -th column has a single character.

1. If the first statement holds, this is represented by the character 'A'.
2. If the second holds, this is represented by the character 'O'.
3. If the third holds, this is represented by the character 'X'.
4. The diagonal of this matrix will only contain the character '-'.

Note that it is possible that a pair of nodes may satisfy multiple statements, in which case, the character given will represent one of the true statements for that pair. This matrix is also guaranteed to be symmetric.

You would like to know if there is a directed graph that is consistent with this matrix. If it is impossible, print the integer -1. Otherwise, print the minimum number of edges that could be consistent with this information.

The first line will contain an integer $n$ ( $1<=n<=47$ ), the number of nodes.

The next $n$ lines will contain $n$ characters each: the matrix of what you know about the graph connectivity in the format described in the statement.

Print the minimum number of edges that is consistent with the given information, or -1 if it is impossible.

Sample 1: The hidden graph is a strongly connected graph. We can put all four nodes in a cycle.

Sample 2: One valid graph is $3→1→2$ . For each distinct pair, exactly one of $f(u,v),f(v,u)$ holds.