CF913H.Don't Exceed

You generate real numbers $s_{1},s_{2},...,s_{n}$ as follows:

• $s_{0}=0$ ;
• $s_{i}=s_{i-1}+t_{i}$ , where $t_{i}$ is a real number chosen independently uniformly at random between 0 and 1, inclusive.

You are given real numbers $x_{1},x_{2},...,x_{n}$ . You are interested in the probability that $s_{i}<=x_{i}$ is true for all $i$ simultaneously.

It can be shown that this can be represented as 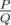, where $P$ and $Q$ are coprime integers, and 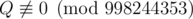. Print the value of $P·Q^{-1}$ modulo $998244353$ .

The first line contains integer $n$ ( $1<=n<=30$ ).

The next $n$ lines contain real numbers $x_{1},x_{2},...,x_{n}$ , given with at most six digits after the decimal point ( 0<x_{i}<=n ).

Print a single integer, the answer to the problem.

In the first example, the sought probability is 1 since the sum of $i$ real numbers which don't exceed 1 doesn't exceed $i$ .

In the second example, the probability is $x_{1}$ itself.

In the third example, the sought probability is $3/8$ .