CF919F.A Game With Numbers

Imagine that Alice is playing a card game with her friend Bob. They both have exactly $8$ cards and there is an integer on each card, ranging from $0$ to $4$ . In each round, Alice or Bob in turns choose two cards from different players, let them be $a$ and $b$ , where $a$ is the number on the player's card, and $b$ is the number on the opponent's card. It is necessary that $a·b≠0$ . Then they calculate 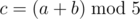and replace the number $a$ with $c$ . The player who ends up with numbers on all $8$ cards being $0$ , wins.

Now Alice wants to know who wins in some situations. She will give you her cards' numbers, Bob's cards' numbers and the person playing the first round. Your task is to determine who wins if both of them choose the best operation in their rounds.

The first line contains one positive integer $T$ ( $1<=T<=100000$ ), denoting the number of situations you need to consider.

The following lines describe those $T$ situations. For each situation:

• The first line contains a non-negative integer $f$ ( $0<=f<=1$ ), where $f=0$ means that Alice plays first and $f=1$ means Bob plays first.
• The second line contains $8$ non-negative integers $a_{1},a_{2},...,a_{8}$ ( $0<=a_{i}<=4$ ), describing Alice's cards.
• The third line contains $8$ non-negative integers $b_{1},b_{2},...,b_{8}$ ( $0<=b_{i}<=4$ ), describing Bob's cards.

We guarantee that if $f=0$ , we have 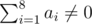. Also when $f=1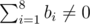$ , holds.

Output $T$ lines. For each situation, determine who wins. Output

• "Alice" (without quotes) if Alice wins.
• "Bob" (without quotes) if Bob wins.
• "Deal" (without quotes) if it gets into a deal, i.e. no one wins.

In the first situation, Alice has all her numbers $0$ . So she wins immediately.

In the second situation, Bob picks the numbers $4$ and $1$ . Because we have 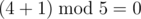, Bob wins after this operation.

In the third situation, Alice picks the numbers $1$ and $4$ . She wins after this operation.

In the fourth situation, we can prove that it falls into a loop.