CF891C.Envy

For a connected undirected weighted graph $G$ , MST (minimum spanning tree) is a subgraph of $G$ that contains all of $G$ 's vertices, is a tree, and sum of its edges is minimum possible.

You are given a graph $G$ . If you run a MST algorithm on graph it would give you only one MST and it causes other edges to become jealous. You are given some queries, each query contains a set of edges of graph $G$ , and you should determine whether there is a MST containing all these edges or not.

The first line contains two integers $n$ , $m$ ( $2<=n,m<=5·10^{5}$ , $n-1<=m$ ) — the number of vertices and edges in the graph and the number of queries.

The $i$ -th of the next $m$ lines contains three integers $u_{i}$ , $v_{i}$ , $w_{i}$ ( $u_{i}≠v_{i}$ , $1<=w_{i}<=5·10^{5}$ ) — the endpoints and weight of the $i$ -th edge. There can be more than one edges between two vertices. It's guaranteed that the given graph is connected.

The next line contains a single integer $q$ ( $1<=q<=5·10^{5}$ ) — the number of queries.

$q$ lines follow, the $i$ -th of them contains the $i$ -th query. It starts with an integer $k_{i}$ ( $1<=k_{i}<=n-1$ ) — the size of edges subset and continues with $k_{i}$ distinct space-separated integers from $1$ to $m$ — the indices of the edges. It is guaranteed that the sum of $k_{i}$ for $1<=i<=q$ does not exceed $5·10^{5}$ .

For each query you should print "YES" (without quotes) if there's a MST containing these edges and "NO" (of course without quotes again) otherwise.

This is the graph of sample:

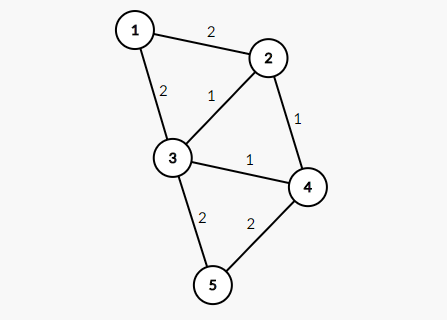Weight of minimum spanning tree on this graph is $6$ .

MST with edges $(1,3,4,6)$ , contains all of edges from the first query, so answer on the first query is "YES".

Edges from the second query form a cycle of length $3$ , so there is no spanning tree including these three edges. Thus, answer is "NO".