CF896C.Willem, Chtholly and Seniorious
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
— Willem...
— What's the matter?
— It seems that there's something wrong with Seniorious...
— I'll have a look...

Seniorious is made by linking special talismans in particular order.
After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.
Seniorious has n pieces of talisman. Willem puts them in a line, the i -th of which is an integer ai .
In order to maintain it, Willem needs to perform m operations.
There are four types of operations:
- 1 l r x : For each i such that l<=i<=r , assign ai+x to ai .
- 2 l r x : For each i such that l<=i<=r , assign x to ai .
- 3 l r x : Print the x -th smallest number in the index range [l,r] , i.e. the element at the x -th position if all the elements ai such that l<=i<=r are taken and sorted into an array of non-decreasing integers. It's guaranteed that 1<=x<=r−l+1 .
- 4 l r x y : Print the sum of the x -th power of ai such that l<=i<=r , modulo y , i.e.
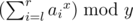 .
.
输入格式
The only line contains four integers n,m,seed,vmax ( 1<=n,m<=105,0<=seed<109+7,1<=vmax<=109 ).
The initial values and operations are generated using following pseudo code:
def rnd():
ret = seed
seed = (seed * 7 + 13) mod 1000000007
return ret
for i = 1 to n:
a[i] = (rnd() mod vmax) + 1
for i = 1 to m:
op = (rnd() mod 4) + 1
l = (rnd() mod n) + 1
r = (rnd() mod n) + 1
if (l > r):
swap(l, r)
if (op == 3):
x = (rnd() mod (r - l + 1)) + 1
else:
x = (rnd() mod vmax) + 1
if (op == 4):
y = (rnd() mod vmax) + 1
Here op is the type of the operation mentioned in the legend.
输出格式
For each operation of types 3 or 4 , output a line containing the answer.
输入输出样例
输入#1
10 10 7 9
输出#1
2 1 0 3
输入#2
10 10 9 9
输出#2
1 1 3 3
说明/提示
In the first example, the initial array is 8,9,7,2,3,1,5,6,4,8 .
The operations are:
- 2 6 7 9
- 1 3 10 8
- 4 4 6 2 4
- 1 4 5 8
- 2 1 7 1
- 4 7 9 4 4
- 1 2 7 9
- 4 5 8 1 1
- 2 5 7 5
- 4 3 10 8 5