CF901B.GCD of Polynomials
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Suppose you have two polynomials 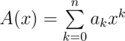 and
and 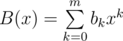 . Then polynomial
. Then polynomial 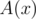 can be uniquely represented in the following way:
can be uniquely represented in the following way:
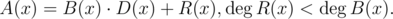 This can be done using long division. Here,
This can be done using long division. Here, 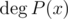 denotes the degree of polynomial P(x) .
denotes the degree of polynomial P(x) . 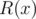 is called the remainder of division of polynomial
is called the remainder of division of polynomial 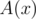 by polynomial
by polynomial 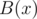 , it is also denoted as
, it is also denoted as 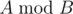 .
.
Since there is a way to divide polynomials with remainder, we can define Euclid's algorithm of finding the greatest common divisor of two polynomials. The algorithm takes two polynomials 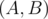 . If the polynomial
. If the polynomial 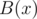 is zero, the result is
is zero, the result is 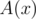 , otherwise the result is the value the algorithm returns for pair
, otherwise the result is the value the algorithm returns for pair 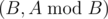 . On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
. On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
You are given an integer n . You have to build two polynomials with degrees not greater than n , such that their coefficients are integers not exceeding 1 by their absolute value, the leading coefficients (ones with the greatest power of x ) are equal to one, and the described Euclid's algorithm performs exactly n steps finding their greatest common divisor. Moreover, the degree of the first polynomial should be greater than the degree of the second. By a step of the algorithm we mean the transition from pair 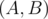 to pair
to pair 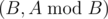 .
.
输入格式
You are given a single integer n ( 1<=n<=150 ) — the number of steps of the algorithm you need to reach.
输出格式
Print two polynomials in the following format.
In the first line print a single integer m ( 0<=m<=n ) — the degree of the polynomial.
In the second line print m+1 integers between −1 and 1 — the coefficients of the polynomial, from constant to leading.
The degree of the first polynomial should be greater than the degree of the second polynomial, the leading coefficients should be equal to 1 . Euclid's algorithm should perform exactly n steps when called using these polynomials.
If there is no answer for the given n , print -1.
If there are multiple answer, print any of them.
输入输出样例
输入#1
1
输出#1
1 0 1 0 1
输入#2
2
输出#2
2 -1 0 1 1 0 1
说明/提示
In the second example you can print polynomials x2−1 and x . The sequence of transitions is
(x2−1,x)→(x,−1)→(−1,0). There are two steps in it.