CF1924C.Fractal Origami
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You have a square piece of paper with a side length equal to 1 unit. In one operation, you fold each corner of the square to the center of the paper, thus forming another square with a side length equal to 21 units. By taking this square as a new square, you do the operation again and repeat this process a total of N times.
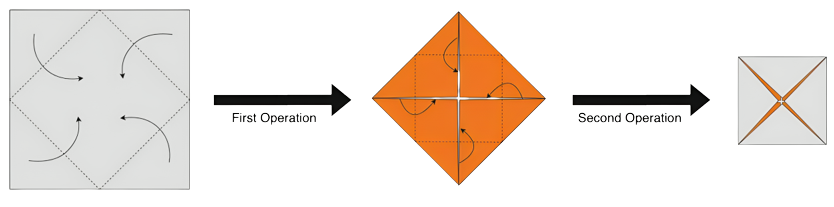 Performing operations for N=2 .After performing the set of operations, you open the paper with the same side up you started with and see some crease lines on it. Every crease line is one of two types: a mountain or a valley. A mountain is when the paper folds outward, and a valley is when the paper folds inward.
Performing operations for N=2 .After performing the set of operations, you open the paper with the same side up you started with and see some crease lines on it. Every crease line is one of two types: a mountain or a valley. A mountain is when the paper folds outward, and a valley is when the paper folds inward.
You calculate the sum of the length of all mountain crease lines on the paper and call it M . Similarly, you calculate for valley crease lines and call it V . You want to find the value of VM .
It can be proved that this value can be represented in the form of A+B2 , where A and B are rational numbers. Let this B be represented as an irreducible fraction qp , your task is to print p∗inv(q) modulo 999999893 (note the unusual modulo), where inv(q) is the modular inverse of q .
输入格式
Each test contains multiple test cases. The first line contains the number of test cases t ( 1≤t≤104 ). Description of the test cases follows.
The only line of each test case contains an integer N ( 1≤N≤109 ), the number of operations you perform on the square paper.
输出格式
For each test case, print on a new line the required answer.
输入输出样例
输入#1
3 1 2 3
输出#1
0 1 714285638
说明/提示
The blue lines in the given figures represent mountain crease lines, and the green lines represent valley crease lines.

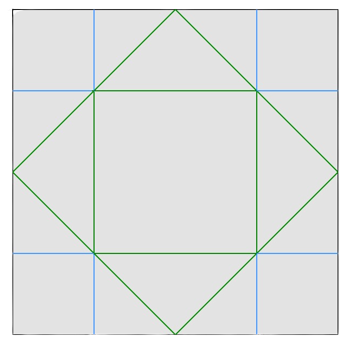 Crease lines after 1 operation (VM=0) .Crease lines after 2 operations (VM=2−1) .
Crease lines after 1 operation (VM=0) .Crease lines after 2 operations (VM=2−1) .