CF859D.Third Month Insanity
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
The annual college sports-ball tournament is approaching, which for trademark reasons we'll refer to as Third Month Insanity. There are a total of 2N teams participating in the tournament, numbered from 1 to 2N . The tournament lasts N rounds, with each round eliminating half the teams. The first round consists of 2N−1 games, numbered starting from 1 . In game i , team 2⋅i−1 will play against team 2⋅i . The loser is eliminated and the winner advances to the next round (there are no ties). Each subsequent round has half as many games as the previous round, and in game i the winner of the previous round's game 2⋅i−1 will play against the winner of the previous round's game 2⋅i .
Every year the office has a pool to see who can create the best bracket. A bracket is a set of winner predictions for every game. For games in the first round you may predict either team to win, but for games in later rounds the winner you predict must also be predicted as a winner in the previous round. Note that the bracket is fully constructed before any games are actually played. Correct predictions in the first round are worth 1 point, and correct predictions in each subsequent round are worth twice as many points as the previous, so correct predictions in the final game are worth 2N−1 points.
For every pair of teams in the league, you have estimated the probability of each team winning if they play against each other. Now you want to construct a bracket with the maximum possible expected score.
输入格式
Input will begin with a line containing N ( 2<=N<=6 ).
2N lines follow, each with 2N integers. The j -th column of the i -th row indicates the percentage chance that team i will defeat team j , unless i=j , in which case the value will be 0 . It is guaranteed that the i -th column of the j -th row plus the j -th column of the i -th row will add to exactly 100 .
输出格式
Print the maximum possible expected score over all possible brackets. Your answer must be correct to within an absolute or relative error of 10−9 .
Formally, let your answer be a , and the jury's answer be b . Your answer will be considered correct, if 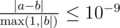 .
.
输入输出样例
输入#1
2 0 40 100 100 60 0 40 40 0 60 0 45 0 60 55 0
输出#1
1.75
输入#2
3 0 0 100 0 100 0 0 0 100 0 100 0 0 0 100 100 0 0 0 100 100 0 0 0 100 100 0 0 0 0 100 100 0 100 0 100 0 0 100 0 100 100 100 100 100 0 0 0 100 0 100 0 0 100 0 0 100 0 100 0 100 100 100 0
输出#2
12
输入#3
2 0 21 41 26 79 0 97 33 59 3 0 91 74 67 9 0
输出#3
3.141592
说明/提示
In the first example, you should predict teams 1 and 4 to win in round 1 , and team 1 to win in round 2 . Recall that the winner you predict in round 2 must also be predicted as a winner in round 1 .