CF862E.Mahmoud and Ehab and the function

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Dr. Evil is interested in math and functions, so he gave Mahmoud and Ehab array $a$ of length $n$ and array $b$ of length $m$ . He introduced a function $f(j)$ which is defined for integers $j$ , which satisfy $0<=j<=m-n$ . Suppose, $c_{i}=a_{i}-b_{i+j}$ . Then $f(j)=|c_{1}-c_{2}+c_{3}-c_{4}...\ c_{n}|$ . More formally, .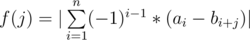

Dr. Evil wants Mahmoud and Ehab to calculate the minimum value of this function over all valid $j$ . They found it a bit easy, so Dr. Evil made their task harder. He will give them $q$ update queries. During each update they should add an integer $x_{i}$ to all elements in $a$ in range $[l_{i};r_{i}]$ i.e. they should add $x_{i}$ to $a_{li},a_{li}+1,...\ ,a_{ri}$ and then they should calculate the minimum value of $f(j)$ for all valid $j$ .

Please help Mahmoud and Ehab.

输入格式

The first line contains three integers $n,m$ and $q$ ( $1<=n<=m<=10^{5}$ , $1<=q<=10^{5}$ ) — number of elements in $a$ , number of elements in $b$ and number of queries, respectively.

The second line contains $n$ integers $a_{1},a_{2},...,a_{n}$ . ( $-10^{9}<=a_{i}<=10^{9}$ ) — elements of $a$ .

The third line contains $m$ integers $b_{1},b_{2},...,b_{m}$ . ( $-10^{9}<=b_{i}<=10^{9}$ ) — elements of $b$ .

Then $q$ lines follow describing the queries. Each of them contains three integers $l_{i}$ $r_{i}$ $x_{i}$ ( $1<=l_{i}<=r_{i}<=n$ , $-10^{9}<=x<=10^{9}$ ) — range to be updated and added value.

输出格式

The first line should contain the minimum value of the function $f$ before any update.

Then output $q$ lines, the $i$ -th of them should contain the minimum value of the function $f$ after performing the $i$ -th update .

输入输出样例

输入#1

5 6 3
1 2 3 4 5
1 2 3 4 5 6
1 1 10
1 1 -9
1 5 -1

输出#1

说明/提示

For the first example before any updates it's optimal to choose $j=0$ , $f(0)=|(1-1)-(2-2)+(3-3)-(4-4)+(5-5)|=|0|=0$ .

After the first update $a$ becomes ${11,2,3,4,5}$ and it's optimal to choose $j=1$ , $f(1)=|(11-2)-(2-3)+(3-4)-(4-5)+(5-6)=|9|=9$ .

After the second update $a$ becomes ${2,2,3,4,5}$ and it's optimal to choose $j=1$ , $f(1)=|(2-2)-(2-3)+(3-4)-(4-5)+(5-6)|=|0|=0$ .

After the third update $a$ becomes ${1,1,2,3,4}$ and it's optimal to choose $j=0$ , $f(0)=|(1-1)-(1-2)+(2-3)-(3-4)+(4-5)|=|0|=0$ .

首页