CF868G.El Toll Caves

The prehistoric caves of El Toll are located in Moià (Barcelona). You have heard that there is a treasure hidden in one of $n$ possible spots in the caves. You assume that each of the spots has probability $1/n$ to contain a treasure.

You cannot get into the caves yourself, so you have constructed a robot that can search the caves for treasure. Each day you can instruct the robot to visit exactly $k$ distinct spots in the caves. If none of these spots contain treasure, then the robot will obviously return with empty hands. However, the caves are dark, and the robot may miss the treasure even when visiting the right spot. Formally, if one of the visited spots does contain a treasure, the robot will obtain it with probability $1/2$ , otherwise it will return empty. Each time the robot searches the spot with the treasure, his success probability is independent of all previous tries (that is, the probability to miss the treasure after searching the right spot $x$ times is $1/2^{x}$ ).

What is the expected number of days it will take to obtain the treasure if you choose optimal scheduling for the robot? Output the answer as a rational number modulo $10^{9}+7$ . Formally, let the answer be an irreducible fraction $P/Q$ , then you have to output 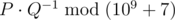. It is guaranteed that $Q$ is not divisible by $10^{9}+7$ .

The first line contains the number of test cases $T$ ( $1<=T<=1000$ ).

Each of the next $T$ lines contains two integers $n$ and $k$ ( $1<=k<=n<=5·10^{8}$ ).

For each test case output the answer in a separate line.

In the first case the robot will repeatedly search in the only spot. The expected number of days in this case is 2. Note that in spite of the fact that we know the treasure spot from the start, the robot still has to search there until he succesfully recovers the treasure.

In the second case the answer can be shown to be equal to $7/2$ if we search the two spots alternatively. In the third case the answer is $25/9$ .