CF869D.The Overdosing Ubiquity

The fundamental prerequisite for justice is not to be correct, but to be strong. That's why justice is always the victor.

The Cinderswarm Bee. Koyomi knows it.

The bees, according to their nature, live in a tree. To be more specific, a complete binary tree with $n$ nodes numbered from $1$ to $n$ . The node numbered $1$ is the root, and the parent of the $i$ -th ( $2<=i<=n$ ) node is 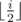. Note that, however, all edges in the tree are undirected.

Koyomi adds $m$ extra undirected edges to the tree, creating more complication to trick the bees. And you're here to count the number of simple paths in the resulting graph, modulo $10^{9}+7$ . A simple path is an alternating sequence of adjacent nodes and undirected edges, which begins and ends with nodes and does not contain any node more than once. Do note that a single node is also considered a valid simple path under this definition. Please refer to the examples and notes below for instances.

The first line of input contains two space-separated integers $n$ and $m$ ( $1<=n<=10^{9}$ , $0<=m<=4$ ) — the number of nodes in the tree and the number of extra edges respectively.

The following $m$ lines each contains two space-separated integers $u$ and $v$ ( $1<=u,v<=n$ , $u≠v$ ) — describing an undirected extra edge whose endpoints are $u$ and $v$ .

Note that there may be multiple edges between nodes in the resulting graph.

Output one integer — the number of simple paths in the resulting graph, modulo $10^{9}+7$ .

In the first example, the paths are: $(1)$ ; $(2)$ ; $(3)$ ; $(1,2)$ ; $(2,1)$ ; $(1,3)$ ; $(3,1)$ ; $(2,1,3)$ ; $(3,1,2)$ . (For the sake of clarity, the edges between nodes are omitted since there are no multiple edges in this case.)

In the second example, the paths are: $(1)$ ; $(1,2)$ ; $(1,2,3)$ ; $(1,3)$ ; $(1,3,2)$ ; and similarly for paths starting with $2$ and $3$ . ( $5×3=15$ paths in total.)

In the third example, the paths are: $(1)$ ; $(2)$ ; any undirected edge connecting the two nodes travelled in either direction. ( $2+5×2=12$ paths in total.)