CF870D.Something with XOR Queries

This is an interactive problem.

Jury has hidden a permutation $p$ of integers from $0$ to $n-1$ . You know only the length $n$ . Remind that in permutation all integers are distinct.

Let $b$ be the inverse permutation for $p$ , i.e. $p_{bi}=i$ for all $i$ . The only thing you can do is to ask xor of elements $p_{i}$ and $b_{j}$ , printing two indices $i$ and $j$ (not necessarily distinct). As a result of the query with indices $i$ and $j$ you'll get the value , where denotes the xor operation. You can find the description of xor operation in notes.

Note that some permutations can remain indistinguishable from the hidden one, even if you make all possible $n^{2}$ queries. You have to compute the number of permutations indistinguishable from the hidden one, and print one of such permutations, making no more than $2n$ queries.

The hidden permutation does not depend on your queries.

The first line contains single integer $n$ ( $1<=n<=5000$ ) — the length of the hidden permutation. You should read this integer first.

When your program is ready to print the answer, print three lines.

In the first line print "!".

In the second line print single integer $answers_cnt$ — the number of permutations indistinguishable from the hidden one, including the hidden one.

In the third line print $n$ integers $p_{0},p_{1},...,p_{n-1}$ ( $0<=p_{i}<n$ , all $p_{i}$ should be distinct) — one of the permutations indistinguishable from the hidden one.

Your program should terminate after printing the answer.

Interaction

To ask about xor of two elements, print a string "? i j", where $i$ and $j$ — are integers from $0$ to $n-1$ — the index of the permutation element and the index of the inverse permutation element you want to know the xor-sum for. After that print a line break and make flush operation.

After printing the query your program should read single integer — the value of .

For a permutation of length $n$ your program should make no more than $2n$ queries about xor-sum. Note that printing answer doesn't count as a query. Note that you can't ask more than $2n$ questions. If you ask more than $2n$ questions or at least one incorrect question, your solution will get "Wrong answer".

If at some moment your program reads -1 as an answer, it should immediately exit (for example, by calling exit(0)). You will get "Wrong answer" in this case, it means that you asked more than $2n$ questions, or asked an invalid question. If you ignore this, you can get other verdicts since your program will continue to read from a closed stream.

Your solution will get "Idleness Limit Exceeded", if you don't print anything or forget to flush the output, including for the final answer .

To flush you can use (just after printing line break):

• fflush(stdout) in C++;
• System.out.flush() in Java;
• stdout.flush() in Python;
• flush(output) in Pascal;
• For other languages see the documentation.

Hacking

For hacking use the following format:

$n$

$p_{0}$ $p_{1}$ ... $p_{n-1}$

Contestant programs will not be able to see this input.

xor operation, or bitwise exclusive OR, is an operation performed over two integers, in which the $i$ -th digit in binary representation of the result is equal to $1$ if and only if exactly one of the two integers has the $i$ -th digit in binary representation equal to $1$ . For more information, see here.

In the first example $p=[0,1,2]$ , thus $b=[0,1,2]$ , the values are correct for the given $i,j$ . There are no other permutations that give the same answers for the given queries.

The answers for the queries are:

• ,
• ,
• ,
• ,
• ,
• .

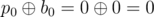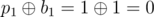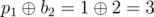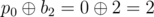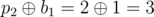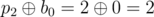In the second example $p=[3,1,2,0]$ , and $b=[3,1,2,0]$ , the values match for all pairs $i,j$ . But there is one more suitable permutation $p=[0,2,1,3]$ , $b=[0,2,1,3]$ that matches all $n^{2}$ possible queries as well. All other permutations do not match even the shown queries.