CF838F.Expected Earnings
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
You are playing a game with a bag of red and black balls. Initially, you are told that the bag has n balls total. In addition, you are also told that the bag has probability pi/106 of containing exactly i red balls.
You now would like to buy balls from this bag. You really like the color red, so red balls are worth a unit of 1 , while black balls are worth nothing. To buy a ball, if there are still balls in the bag, you pay a cost c with 0<=c<=1 , and draw a ball randomly from the bag. You can choose to stop buying at any point (and you can even choose to not buy anything at all).
Given that you buy optimally to maximize the expected profit (i.e. # red balls - cost needed to obtain them), print the maximum expected profit.
输入格式
The first line of input will contain two integers n,X ( 1<=n<=10000 , 0<=X<=106 ).
The next line of input will contain n+1 integers p0,p1,... pn ( 0<=pi<=106 , 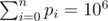 )
)
The value of c can be computed as 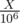 .
.
输出格式
Print a single floating point number representing the optimal expected value.
Your answer will be accepted if it has absolute or relative error at most 10−9 . More specifically, if your answer is a and the jury answer is b , your answer will be accepted if 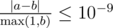 .
.
输入输出样例
输入#1
3 200000 250000 250000 250000 250000
输出#1
0.9000000000
说明/提示
Here, there is equal probability for the bag to contain 0,1,2,3 red balls. Also, it costs 0.2 to draw a ball from the bag.