CF850D.Tournament Construction

Ivan is reading a book about tournaments. He knows that a tournament is an oriented graph with exactly one oriented edge between each pair of vertices. The score of a vertex is the number of edges going outside this vertex.

Yesterday Ivan learned Landau's criterion: there is tournament with scores $d_{1}<=d_{2}<=...<=d_{n}$ if and only if 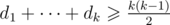for all 1<=k<n and .

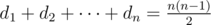Now, Ivan wanna solve following problem: given a set of numbers $S={a_{1},a_{2},...,a_{m}}$ , is there a tournament with given set of scores? I.e. is there tournament with sequence of scores $d_{1},d_{2},...,d_{n}$ such that if we remove duplicates in scores, we obtain the required set ${a_{1},a_{2},...,a_{m}}$ ?

Find a tournament with minimum possible number of vertices.

The first line contains a single integer $m$ ( $1<=m<=31$ ).

The next line contains $m$ distinct integers $a_{1},a_{2},...,a_{m}$ ( $0<=a_{i}<=30$ ) — elements of the set $S$ . It is guaranteed that all elements of the set are distinct.

If there are no such tournaments, print string "=(" (without quotes).

Otherwise, print an integer $n$ — the number of vertices in the tournament.

Then print $n$ lines with $n$ characters — matrix of the tournament. The $j$ -th element in the $i$ -th row should be $1$ if the edge between the $i$ -th and the $j$ -th vertices is oriented towards the $j$ -th vertex, and $0$ otherwise. The main diagonal should contain only zeros.