CF852C.Property

Bill is a famous mathematician in BubbleLand. Thanks to his revolutionary math discoveries he was able to make enough money to build a beautiful house. Unfortunately, for not paying property tax on time, court decided to punish Bill by making him lose a part of his property.

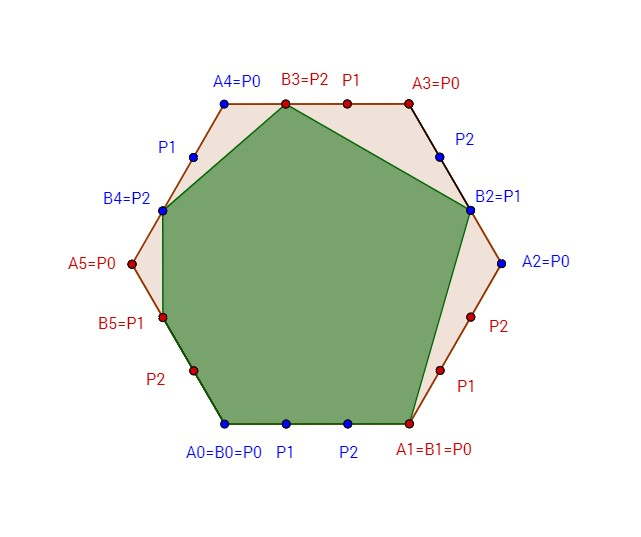
Bill’s property can be observed as a convex regular $2n$ -sided polygon $A_{0}\ A_{1}...\ A_{2n-1}\ A_{2n},\ A_{2n}=\ A_{0}$ , with sides of the exactly 1 meter in length.

Court rules for removing part of his property are as follows:

• Split every edge $A_{k}\ A_{k+1},\ k=0...\ 2n-1$ in $n$ equal parts of size $1/n$ with points $P_{0},P_{1},...,P_{n-1}$
• On every edge $A_{2k}\ A_{2k+1},\ k=0...\ n-1$ court will choose one point $B_{2k}=\ P_{i}$ for some $i=0,...,\ n-1$ such that
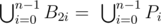
• On every edge $A_{2k+1}A_{2k+2},\ k=0...n-1$ Bill will choose one point $B_{2k+1}=\ P_{i}$ for some $i=0,...,\ n-1$ such that
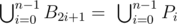
• Bill gets to keep property inside of $2n$ -sided polygon $B_{0}\ B_{1}...\ B_{2n-1}$

Luckily, Bill found out which $B_{2k}$ points the court chose. Even though he is a great mathematician, his house is very big and he has a hard time calculating. Therefore, he is asking you to help him choose points so he maximizes area of property he can keep.

The first line contains one integer number $n\ (2<=n<=50000)$ , representing number of edges of $2n$ -sided polygon.

The second line contains $n$ distinct integer numbers $B_{2k}\ (0<=B_{2k}<=n-1,\ k=0...\ n-1)$ separated by a single space, representing points the court chose. If $B_{2k}=i$ , the court chose point $P_{i}$ on side $A_{2k}\ A_{2k+1}$ .

Output contains $n$ distinct integers separated by a single space representing points $B_{1},B_{3},...,B_{2n-1}$ Bill should choose in order to maximize the property area. If there are multiple solutions that maximize the area, return any of them.

To maximize area Bill should choose points: $B_{1}=P_{0}$ , $B_{3}=P_{2}$ , $B_{5}=P_{1}$