CF809E.Surprise me!

Tired of boring dates, Leha and Noora decided to play a game.

Leha found a tree with $n$ vertices numbered from $1$ to $n$ . We remind you that tree is an undirected graph without cycles. Each vertex $v$ of a tree has a number $a_{v}$ written on it. Quite by accident it turned out that all values written on vertices are distinct and are natural numbers between $1$ and $n$ .

The game goes in the following way. Noora chooses some vertex $u$ of a tree uniformly at random and passes a move to Leha. Leha, in his turn, chooses (also uniformly at random) some vertex $v$ from remaining vertices of a tree $(v≠u)$ . As you could guess there are $n(n-1)$ variants of choosing vertices by players. After that players calculate the value of a function $f(u,v)=φ(a_{u}·a_{v})$ $·$ $d(u,v)$ of the chosen vertices where $φ(x)$ is Euler's totient function and $d(x,y)$ is the shortest distance between vertices $x$ and $y$ in a tree.

Soon the game became boring for Noora, so Leha decided to defuse the situation and calculate expected value of function $f$ over all variants of choosing vertices $u$ and $v$ , hoping of at least somehow surprise the girl.

Leha asks for your help in calculating this expected value. Let this value be representable in the form of an irreducible fraction 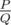. To further surprise Noora, he wants to name her the value .

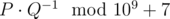Help Leha!

The first line of input contains one integer number $n$ $(2<=n<=2·10^{5})$ — number of vertices in a tree.

The second line contains $n$ different numbers $a_{1},a_{2},...,a_{n}$ $(1<=a_{i}<=n)$ separated by spaces, denoting the values written on a tree vertices.

Each of the next $n-1$ lines contains two integer numbers $x$ and $y$ $(1<=x,y<=n)$ , describing the next edge of a tree. It is guaranteed that this set of edges describes a tree.

In a single line print a number equal to $P·Q^{-1}$ modulo $10^{9}+7$ .

Euler's totient function $φ(n)$ is the number of such $i$ that $1<=i<=n$ ,and $gcd(i,n)=1$ , where $gcd(x,y)$ is the greatest common divisor of numbers $x$ and $y$ .

There are $6$ variants of choosing vertices by Leha and Noora in the first testcase:

• $u=1$ , $v=2$ , $f(1,2)=φ(a_{1}·a_{2})·d(1,2)=φ(1·2)·1=φ(2)=1$
• $u=2$ , $v=1$ , $f(2,1)=f(1,2)=1$
• $u=1$ , $v=3$ , $f(1,3)=φ(a_{1}·a_{3})·d(1,3)=φ(1·3)·2=2φ(3)=4$
• $u=3$ , $v=1$ , $f(3,1)=f(1,3)=4$
• $u=2$ , $v=3$ , $f(2,3)=φ(a_{2}·a_{3})·d(2,3)=φ(2·3)·1=φ(6)=2$
• $u=3$ , $v=2$ , $f(3,2)=f(2,3)=2$

Expected value equals to 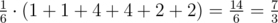. The value Leha wants to name Noora is $7·3^{-1}=7·333333336=333333338$ .

In the second testcase expected value equals to 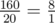, so Leha will have to surprise Hoora by number $8·1^{-1}=8$ .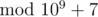