CF793C.Mice problem
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Igor the analyst fell asleep on the work and had a strange dream. In the dream his desk was crowded with computer mice, so he bought a mousetrap to catch them.
The desk can be considered as an infinite plane, then the mousetrap is a rectangle which sides are parallel to the axes, and which opposite sides are located in points (x1,y1) and (x2,y2) .
Igor wants to catch all mice. Igor has analysed their behavior and discovered that each mouse is moving along a straight line with constant speed, the speed of the i -th mouse is equal to (vix,viy) , that means that the x coordinate of the mouse increases by vix units per second, while the y coordinates increases by viy units. The mousetrap is open initially so that the mice are able to move freely on the desk. Igor can close the mousetrap at any moment catching all the mice that are strictly inside the mousetrap.
Igor works a lot, so he is busy in the dream as well, and he asks you to write a program that by given mousetrap's coordinates, the initial coordinates of the mice and their speeds determines the earliest time moment in which he is able to catch all the mice. Please note that Igor can close the mousetrap only once.
输入格式
The first line contains single integer n ( 1<=n<=100000 ) — the number of computer mice on the desk.
The second line contains four integers x1 , y1 , x2 and y2 ( 0<=x1<=x2<=100000 ), ( 0<=y1<=y2<=100000 ) — the coordinates of the opposite corners of the mousetrap.
The next n lines contain the information about mice.
The i -th of these lines contains four integers rix , riy , vix and viy , ( 0<=rix,riy<=100000 , −100000<=vix,viy<=100000 ), where (rix,riy) is the initial position of the mouse, and (vix,viy) is its speed.
输出格式
In the only line print minimum possible non-negative number t such that if Igor closes the mousetrap at t seconds from the beginning, then all the mice are strictly inside the mousetrap. If there is no such t , print -1.
Your answer is considered correct if its absolute or relative error doesn't exceed 10−6 .
Formally, let your answer be a , and the jury's answer be b . Your answer is considered correct if 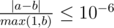 .
.
输入输出样例
输入#1
4 7 7 9 8 3 5 7 5 7 5 2 4 3 3 7 8 6 6 3 2
输出#1
0.57142857142857139685
输入#2
4 7 7 9 8 0 3 -5 4 5 0 5 4 9 9 -1 -6 10 5 -7 -10
输出#2
-1
说明/提示
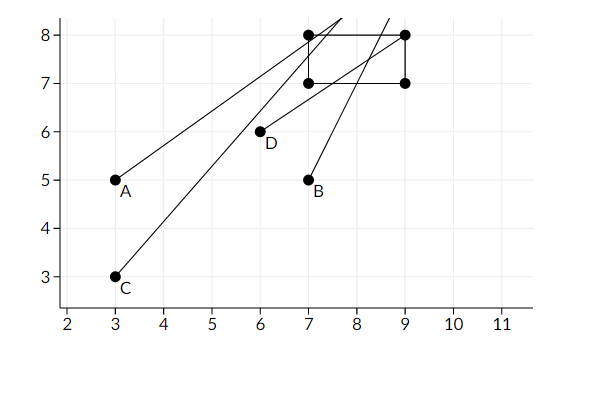
Here is a picture of the first sample
Points A, B, C, D - start mice positions, segments are their paths.
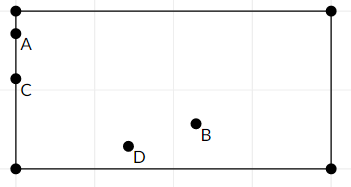
Then, at first time when all mice will be in rectangle it will be looks like this:
Here is a picture of the second sample
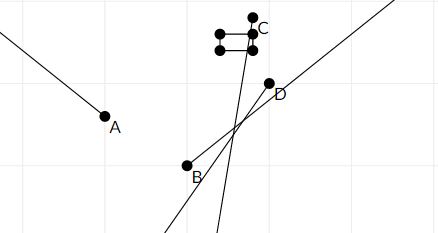
Points A, D, B will never enter rectangle.