CF771E.Bear and Rectangle Strips

Limak has a grid that consists of $2$ rows and $n$ columns. The $j$ -th cell in the $i$ -th row contains an integer $t_{i,j}$ which can be positive, negative or zero.

A non-empty rectangle of cells is called nice if and only if the sum of numbers in its cells is equal to $0$ .

Limak wants to choose some nice rectangles and give them to his friends, as gifts. No two chosen rectangles should share a cell. What is the maximum possible number of nice rectangles Limak can choose?

The first line of the input contains an integer $n$ ( $1<=n<=300000$ ) — the number of columns in the grid.

The next two lines contain numbers in the grid. The $i$ -th of those two lines contains $n$ integers $t_{i,1},t_{i,2},...,t_{i,n}$ ( $-10^{9}<=t_{i,j}<=10^{9}$ ).

Print one integer, denoting the maximum possible number of cell-disjoint nice rectangles.

In the first sample, there are four nice rectangles:

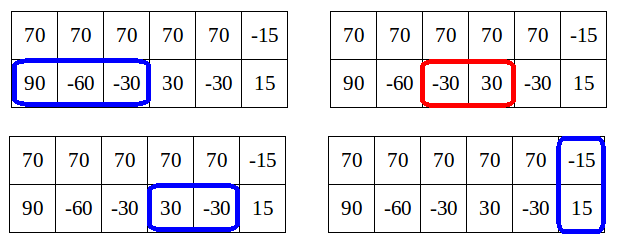Limak can't choose all of them because they are not disjoint. He should take three nice rectangles: those denoted as blue frames on the drawings.

In the second sample, it's optimal to choose six nice rectangles, each consisting of one cell with a number $0$ .

In the third sample, the only nice rectangle is the whole grid — the sum of all numbers is $0$ . Clearly, Limak can choose at most one nice rectangle, so the answer is $1$ .