CF771F.Bear and Isomorphic Points
普及/提高-
通过率:0%
AC君温馨提醒
该题目为【codeforces】题库的题目,您提交的代码将被提交至codeforces进行远程评测,并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供,我们无法保证该服务的稳定性,若提交后无反应,请等待一段时间后再进行重试。
题目描述
Bearland is a big square on the plane. It contains all points with coordinates not exceeding 106 by the absolute value.
There are n houses in Bearland. The i -th of them is located at the point (xi,yi) . The n points are distinct, but some subsets of them may be collinear.
Bear Limak lives in the first house. He wants to destroy his house and build a new one somewhere in Bearland.
Bears don't like big changes. For every three points (houses) pi , pj and pk , the sign of their cross product (pj−pi)×(pk−pi) should be the same before and after the relocation. If it was negative/positive/zero, it should still be negative/positive/zero respectively. This condition should be satisfied for all triples of indices (i,j,k) , possibly equal to each other or different than 1 . Additionally, Limak isn't allowed to build the house at the point where some other house already exists (but it can be the point where his old house was).
In the formula above, we define the difference and the cross product of points (ax,ay) and (bx,by) as:
(ax,ay)−(bx,by)=(ax−bx,ay−by), (ax,ay)×(bx,by)=ax⋅by−ay⋅bx. Consider a set of possible new placements of Limak's house. Your task is to find the area of that set of points.
Formally, let's say that Limak chooses the new placement randomly (each coordinate is chosen independently uniformly at random from the interval [−106,106] ). Let p denote the probability of getting the allowed placement of new house. Let S denote the area of Bearland ( S=4⋅1012 ). Your task is to find p⋅S .
输入格式
The first line of the input contains an integer T ( 1<=T<=500 ) — the number of test cases. The description of the test cases follows.
The first line of the description of a test case contains an integer n ( 3<=n<=200000 ) — the number of houses.
The i -th of the next n lines contains two integers xi and yi ( −106<=xi,yi<=106 ) — coordinates of the i -th house. No two houses are located at the same point in the same test case. Limak lives in the first house.
The sum of n won't exceed 200000 .
输出格式
Print one real value, denoting the area of the set of points that are possible new placements of Limak's house.
Your answer will be considered correct if its absolute or relative error doesn't exceed 10−6 . More precisely, let the jury's answer be b , and your answer be a . Then your answer will be accepted if and only if 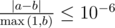 .
.
输入输出样例
输入#1
4 4 5 3 0 1 10 1 3 51 3 -999123 700000 -950000 123456 -950000 987654 3 2 3 10 -1 -4 6 5 1 3 5 2 6 1 4 4 -3 3
输出#1
250.000000000000 100000000000.000000000000 0.000000000000 6.562500000000
说明/提示
In the sample test, there are 4 test cases.
In the first test case, there are four houses and Limak's one is in (5,3) . The set of valid new placements form a triangle with vertices in points (0,1) , (10,1) and (3,51) , without its sides. The area of such a triangle is 250 .
In the second test case, the set of valid new placements form a rectangle of width 50000 and height 2000000 . Don't forget that the new placement must be inside the big square that represents Bearland.
In the third test case, the three given points are collinear. Each cross product is equal to 0 and it should be 0 after the relocation as well. Hence, Limak's new house must lie on the line that goes through the given points. Since it must also be inside the big square, new possible placements are limited to some segment (excluding the two points where the other houses are). The area of any segment is 0 .